Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

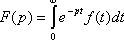 - Это прямое преобразование Лапласа.

Обратное преобразование есть возможность получить функцию-оригинал через известную функцию-изображение :

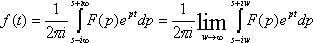, где s – некоторая константа.

Пользоваться формулой для обратного преобразования можно при определенном виде функции F(p), либо для численного нахождения функции-оригинала по известному изображению.

Теоремы разложения.

Известная методика разложения дробно-рациональных функций на сумму элементарных дробей (1)-(4) может быть представлена в виде двух теорем разложения.

Первая теорема разложения. Пусть F(p) – изображение некоторой функции, тогда эта функция представляется в виде ,  k – постоянная, может быть сколь угодно большим числом, , то возможен почленный переход в пространство оригиналов с помощью формулы : .

Вторая теорема разложения. Если изображение представляется дробно-рациональной функцией . Степень числа s меньше степени знаменателя n, знаменатель имеет корни a1, a2, …, a n соответствующий кратности k1, k2, …, kn , при этом k1+ k2 +…+ kn = n. В этом случае оригинал функции определяется по формуле :

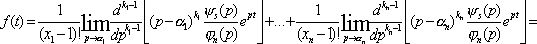
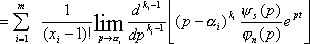                                       (3)

Например :

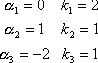
Связь между преобразованиями Фурье и Лапласа.

Преобразование Лапласа имеет вид :

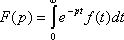                            (1)

На  f(t) наложены условия :

f(t) определена и непрерывна на всем интервале: (-¥ ; ¥ )

f(t) º 0 , t Î (- ¥ ;0)

При  M, S0 >0 , для всех t > 0 выполняется условие |f(t)|<Me S0t

Если отказаться от условий 2 и 3, и считать, что f(t) принимает произвольное значение при t < 0, то вместо (1) можно рассмотреть следующий интеграл :

                            (2)

Формула (2) – двустороннее преобразование Лапласа.

Пусть в (1) и (2)  p =a + in, где a и n – действительные числа.

Предположим, что Re(p) = a = 0, т.е.

Рекомендуем скачать другие рефераты по теме: шпаргалки по психологии, оформление доклада.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата