Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата



связанного с движением в поле электрета внедренных неравновесных носителей заряда; q - заряд неравновесного носителя, м - подвижность неравновесного носителя, п(х,t) - концентрация неравновесных носителей заряда, зависящая от координаты х и времени t, л проводимость диэлектрика.

j(x,t)=лE(x,t)+qмn(x,t)E(x,t).   (62)

В нашей задаче мы пренебрегаем неравновесной проводимостью, поскольку носители прочно удерживаются ловушками и не способны двигаться в электрическом поле. Тогда в (62) ток проводимости будет состоять из одной компоненты - тока собственной проводимости. Выражение (61) примет вид:

    (63)

В воздушном зазоре будет протекать тот же полный ток j(t), но там он будет чистым током смещения, т.к. никаких носителей заряда нет, и не будет зависеть от координаты:

(64)

С другой стороны, на основании формулы (43) . Поверхностный потенциал при релаксации зависит от времени. Дифференцируя Е1 по времени и подставляя в формулу (64), приходим к выражению для полного тока:

    (65)

Проинтегрируем (63) по координате от 0 до s:

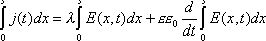
 (предполагается, что л не зависит от координат - однородный диэлектрик). Т.к. 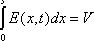, то

   (66)

Из последней формулы видно, что если верхний электрод касается поверхности электрета или напылён на его поверхность, релаксация за счет собственной проводимости наблюдаться не будет: V = 0 и j(t) :=0. Поэтому наличие воздушного зазора является необходимым условием наблюдения релаксации за счет собственной проводимости.

Формулы (65) и (66) дают возможность получить дифференциальное уравнение релаксации поверхностного потенциала, связанной с омической проводимостью. Заменяя в (66) плотность тока по формуле (65), после небольших преобразований приходим к уравнению:

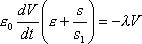   (67)

В случае, когда электрет свободный (нет верхнего электрода, s1→∞), либо при условии, что s1>>s:

  или    (68)

Решение полученного уравнения зависит от того, при каких условиях наблюдается релаксация потенциала - изотермических или при линейном возрастании температуры. Действительно, коэффициент электропроводности диэлектрика л, при Т=сопst постоянен, а с ростом Т увеличивается. Например, если имеется кристаллический диэлектрик с шириной запрещенной зоны ДЕ, то

  .(69)

Рассмотрим случай изотермической релаксации Коэффициент перед dt в уравнении (68) не зависит от времени, тогда общее решение уравнения будет иметь вид;

 Для  определения  постоянной  С  применим начальные условия: при t=0 V = V0. Окончательно получим:

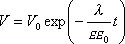  (70)

Решение можно выразить через удельное электрическое сопротивление с=1/л:

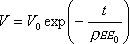  (71)

Рекомендуем скачать другие рефераты по теме: реферат исследование, реферат статус.

Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата