
Интеграл и его применение
| Категория реферата: Рефераты по математике
| Теги реферата: реферат на тему україна, база рефератов
| Добавил(а) на сайт: Bykov.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Примеры :
ò sin 3x cos x dx = 1/2 ò (sin 4x + sin 2x) dx = 1/8 cos 4x – ¼ cos 2x + C
ó x4+3x2+1 ó 1 1
ô———— dx = ô( x2+2 – ——– ) dx = — x2 + 2x – arctg x + C
õ x2+1 õ x2+1 3
Примечание: при решении этого примера хорошо делать многочлены ”углом”.
По частям
Если в заданном виде взять интеграл невозможно, а в то же время, очень легко находится первообразная одного множителя и производная другого, то можно использовать формулу.
(u(x)v(x))’=u’(x)v(x)+u(x)v(x)
u’(x)v(x)=(u(x)v(x)+u(x)v’(x)
Проинтегрируем обе части
ò u’(x)v(x)dx=ò (u(x)v(x))’dx – ò u(x)v’(x)dx
ò u’(x)v(x)dx=u(x)v(x)dx – ò u(x)v’(x)dx
Примеры:
ò x cos (x) dx = ò x dsin x = x sin x – ò sin x dx = x sin x + cos x + C
x = u(x)
cos x = v’(x)
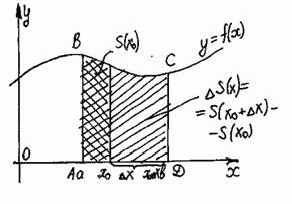
Криволинейная трапеция
Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией.
Способы нахождения площади криволинейной трапеции
Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке [a;b], то площадь соответствующей криволинейной трапеции равна приращению первообразных.
Дано: f(x)– непрерывная неопр. функция, xÎ[a;b].
Доказать: S = F(b) – F(a), где F(x) – первообразная f(x).
Доказательство:
|
|
1) Рассмотрим вспомогательную функцию S(x). Каждому xÎ[a;b] поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой, проходящей через точку с этой абциссой и параллельно оси ординат. Рекомендуем скачать другие рефераты по теме: мцыри сочинение, банк дипломных работ. Категории:Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
 Главная
Главная