Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Символ 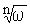не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись 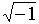, следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i и –i, или одно, то какое именно.

Уравнения высших степеней

Формула 8 определяет все корни двучленного уравнения степени n. Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнения степени n:

anЧ Zn + an–1Ч Zn–1 +...+ a1Ч Z1 + a0 = 0 (9)

Где an,..., a0 – заданные комплексные числа.

В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень. Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.

Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9 всегда может быть представлена в виде произведения:

,

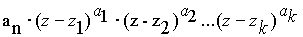Где Z1, Z2,..., ZK– некоторые различные комплексные числа,

а a1,a2,...,ak – натуральные числа, причем:

a1 + a2 + ... + ak = n

Отсюда следует, что числа Z1, Z2,..., ZK являются корнями уравнения 9. При этом говорят, что Z1 является корнем кратности a1, Z2 – корнем кратности a2 и так далее.

Если условиться считать корень уравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел ровно n корней.

Теорема Гаусса и только что сформулированная теорема дают решения о существовании корней, но ничего не говорят о том, как найти эти корни. Если корни первой и второй степени могут быть легко найдены, то для уравнений третей и четвертой степеней формулы громоздки, а для уравнений степени выше четвертой таких формул вообще не существует. Отсутствие общего метода не мешает отыскивать все корни уравнения. Для решения уравнения с целыми коэффициентами часто оказывается полезной следующая теорема: целые корни любого алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.

Докажем эту теорему:

Пусть Z = k – целый корень уравнения

anЧ Zn + an–1Ч Zn–1 +...+ a1Ч Z1 + a0 = 0

с целыми коэффициентами. Тогда

anЧ kn + an–1Ч kn–1 +...+ a1Ч k1 + a0 = 0

a0 = – k(anЧ kn–1 + an–1Ч kn–2 +...+ a1)

Число в скобках, при сделанных предположениях, очевидно, целое, значит k – делитель числа a0.

9.КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ

Рассмотрим уравнение Z2 = a, где a – заданное действительное число, Z – неизвестное.

Это уравнение:

имеет один корень, если a = 0. имеет два действительных корня Z1,2=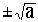, 0. не имеет действительных корней, если a < 0. Но имеет два комплексных корня.

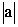Запишем число a в виде a = (– 1)Ч (– a) = i2Ч = i2Ч (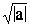)2. Тогда уравнение Z2 = a запишется в виде: Z2 – i2Ч (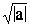)2 = 0

т.е. (Z – iЧ 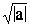)(Z + iЧ 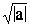) = 0

Следовательно, уравнение имеет два корня: Z1,2 = 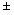iЧ

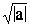
Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.

Категории:

• Математика

Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата