Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами

aЧ Z2 + bЧ Z + c = 0

По известной общей формуле

Z1,2=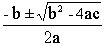 (10)

Итак, при любых действительных a(a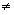0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10

D = b2 – 4Ч aЧ c

положителен , то уравнение aЧ Z2 + bЧ Z + c = 0 два действительных различных корня. Если D = 0, то уравнение aЧ Z2 + bЧ Z + c = 0 имеет один корень. Если D < 0, то уравнение aЧ Z2 + bЧ Z + c = 0 имеет два различных комплексных корня.

Комплексные корни квадратного уравнения обладают такими же свойствами, как и известные нам свойства действительных корней.

Сформулируем основные из них:

Пусть Z1,Z2 – корни квадратного уравнения aЧ Z2 + bЧ Z + c = 0, a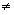0. Тогда справедливы свойства:

Теорема Виета: Z1 + Z2 = –

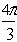
Z1Ч Z2 =

При всех комплексных Z справедлива формула

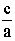
aЧ Z2 + bЧ Z + c = aЧ (Z – Z1)Ч (Z – Z2)

Пример 5:

Z2 – 6·Z + 10 = 0

Д = b2 – 4·a·c

Д = 62 – 4·10 = – 4

– 4 = i2·4

Z1,2 =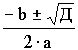

Z1,2 =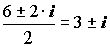

Ответ: Z1 = Z2 = 3 + i

Пример 6:

3·Z2 +2·Z + 1 = 0

Д = b2 – 4·a·c

Д = 4 – 12 = – 8

Д = –1·8 = 8·i2

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата