Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Легко получаем

.

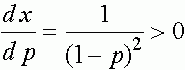В свою очередь, для x>0

.

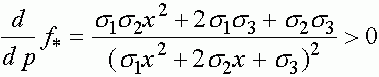Таким образом,

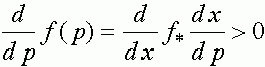
для и функция монотонно растет.

Из монотонности функции вытекает важное следствие. Пусть 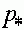и 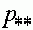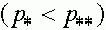- два состояния равновесия и на интервале 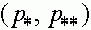других состояний равновесия нет. Предположим, что начальная точка траектории 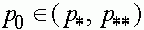. тогда при точки траектории стремятся к одному из состояний равновесия: или к 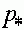, или к .

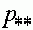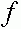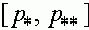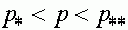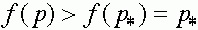Для доказательства заметим сначала, что отображение переводит отрезок в себя. Действительно. в силу монотонности для любого имеем и 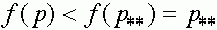, т.е. 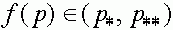. Далее, так как на интервале 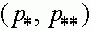нет состояний равновесия (точек, где 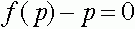), то л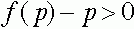ибо либо 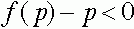для 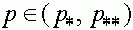. Пусть реализуется первый случай. Тогда 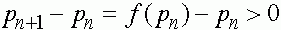. Последовательность 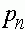монотонно растет и ограничена сверху числом 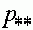. Она сходится. Переходя в равенстве 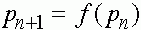к пределу при получим 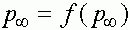. Поскольку на интервале 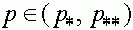отсутствуют состояния равновесия то 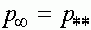, т.е. . Аналогично проверяется, что в случае 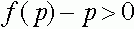для 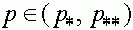точки траектории 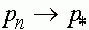. Тем самым, сформулированное следствие доказано.

Доказательство того, что все траектории отображения (17) стремятся к состояниям равновесия теперь легко завершается. Заметим, что крайние точк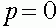и и 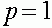отрезка 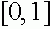являются неподвижными для отображения (17). Если отображение не имеет других неподвижных точек, то все его траектории стремятся к одной и той же неподвижной точке (либо 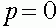, либо 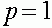. Если существуют другие неподвижные точки, то они разбивают отрезок 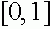на части. Внутри каждой из частей все траектории стремятся к одной из крайних точек разбиения.

Состояния равновесия определяются из уравнения:

.
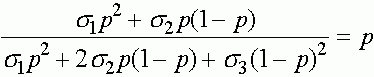Последовательно получаем:

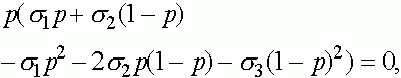
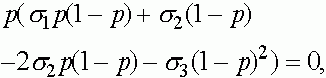
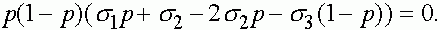
Отсюда получаем, что кроме найденных ранее состояний равновесия 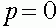и 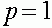может присутствовать еще одно:

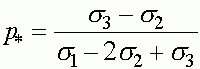. (18)

Соответствующее значение частоты 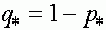суть

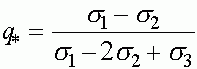. (19)

Поскольку 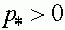и 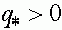, то состояние равновесия (18) существует, если выполнено одно из условий:

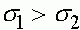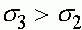, , (20)

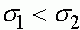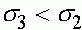, . (21)

В состояниях равновесия 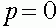и 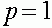генофонд популяции содержит соответственно только аллели A и a. Равновесное состояние, если оно существует, соответствует случаю, когда генофонд содержит оба аллеля. Оно называется равновесным пилиморфизмом.

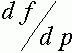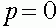Ниже нам потребуются значения производной при и 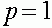. Прямые вычисления показывают, что

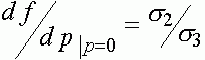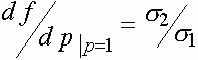, . (22)

Рекомендуем скачать другие рефераты по теме: предмет курсовой работы, бесплатные рефераты и курсовые.





Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата