Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

3) Предполагая для определённости, что ’, получим

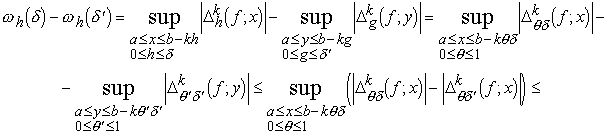
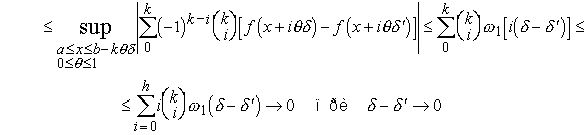
Этим непрерывность функции k() доказана.

4) Используя равенство лемму 2 §1, имеем

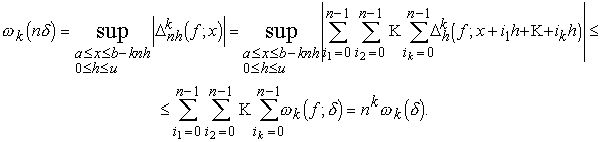Этим неравенство (1.8) доказано. Неравенство (1.8’) следует из монотонности функции k(t) и неравенства (1.8).

5) Используя равенства лемму 1 и лемму 3 §1, получим

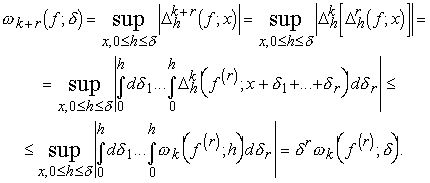
Определение 7. Пусть k-натуральное число. Будем говорить, что функция есть модуль непрерывности k-го порядка функции f, если

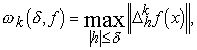
где -конечная разность функции f k-го порядка с шагом h:

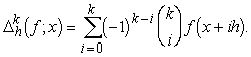
Среди модулей непрерывности всех порядков особенно важное значение имеют случаи k=1 и k=2. Случай k=1 является классическим; вместо мы будем писать просто и называть эту функцию модулем непрерывности; функцию мы будем называть модулем гладкости.

Определение 8. Зададим натуральное число k. Будем говорить, что функция -есть функция сравнения k-го порядка, если она удовлетворяет следующим условиям:

определена для ,

не убывает,

,

Нетрудно показать, что если f 0, то есть функция сравнения k-го порядка (см. Лемму 5 §2).

Определение 9. Зафиксируем натуральное число k и функцию сравнения k-го порядка . Будем говорить, что функция f принадлежит к классу , если найдётся константа С10>0 такая, что

Вместо будем писать просто Hk.

Если для последовательности функций {fn} (n=1,2,...)

где С10 не зависит от n, то будем писать: равномерно относительно n.

Понятие классов является естественным обобщением классов Липшица и классов функций, имеющих ограниченную k-ю производную.

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата