Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Определение 10. Зафиксируем число >0 и обозначим через p наименьшее натуральное число, не меньше чем  (p=-[-]). Будем говорить, что функция принадлежит к классу , если она

1) есть функция сравнения p-го порядка и

2) удовлетворяет условию: существует константа С11>0 такая, что для

Условие 2) является небольшим ослаблением условия “ не убывает”. Функции класса N будут играть основную роль во всём дальнейшем изложении.

Определение 11. Будем говорить, что функция имеет порядок , если найдутся две положительные константы С12 и С13 такие, что для всех t, для которых определены функции и ,

.

При выполнении этих условий будем писать

.

Определение 12. Ядром Дирихле n-го порядка называется функция

(1.10)

Это ядро является тригонометрическим полиномом порядка n и при этом

(1.10’)

Определение 13. Ядром Фейера n-го порядка называется функция

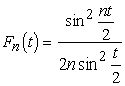(1.11)

Ядро Фейера Fn(t) является средним арифметическим первых n ядер Дирихле, и значит, является тригонометрическим полиномом порядка (n-1). Так что имеют место равенства

(1.11’)

(1.11’’)

где Dk(t)-ядра Дирихле.

Определение 14. Ядром Джексона n-го порядка называется функция

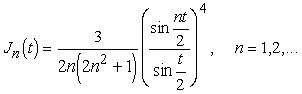(1.12)

Свойства ядер Джексона.

а) При каждом n ядро Jn(t) является чётным неотрицательным тригонометрическим полиномом порядка 2n-2 вида

,

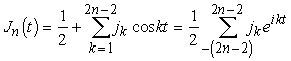где jk=jk(n) - некоторые числа

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата