
Пpиближения непpеpывных пеpиодических фyнкций тpигонометpическими полиномами
| Категория реферата: Рефераты по математике
| Теги реферата: реферати українською, возрождение реферат
| Добавил(а) на сайт: Pogrebnjak.
Предыдущая страница реферата | 9 10 11 12 13 14 15 16 17 18 19 | Следующая страница реферата
Тогда p-1, и так как ![]() -является неубывающей функцией от , то принимая во внимание (2.5) и (2.8), получим
-является неубывающей функцией от , то принимая во внимание (2.5) и (2.8), получим
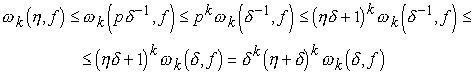
Рассмотрим случай для . Найдём натуральное число p из условий
![]() (2.9)
(2.9)
Тогда p, и так как ![]() -является неубывающей функцией от , то принимая во внимание (2.5) и (2.9), получим
-является неубывающей функцией от , то принимая во внимание (2.5) и (2.9), получим
![]() ,
,
и неравенство (2.6) доказано. Неравенство (2.7) вытекает из (2.6), так как для 0<
Неравенство (2.7) показывает, что для любой f0 и любого натурального k
![]() (2.10)
(2.10)
Лемма доказана.
ЛЕММА 6. Пусть f имеет r-ю производную f(r). Тогда
![]() (2.11)
(2.11)
и для любого натурального k
![]() (2.12)
(2.12)
Доказательство: Оба неравенства непосредственно вытекают из формулы
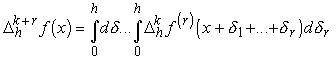
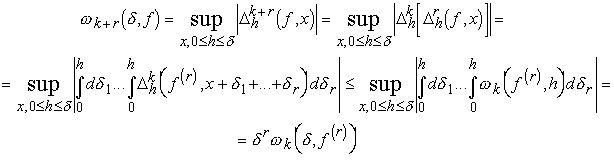 Если k=0, то мы получаем формулу (2.11). Лемма доказана.
Если k=0, то мы получаем формулу (2.11). Лемма доказана.
§3. Обобщение теоремы Джексона.
Здесь будет получено небольшое усиление теоремы Джексона о наилучших приближениях периодических функций тригонометрическими полиномами.
Лемма 7. Пусть дано натуральное число k. Существует последовательность ядер{Kn(t)}(n=0,1,...), где Kn(t) есть тригонометрический полином порядка не выше n, удовлетворяющая условиям:
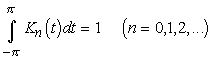 (3.1)
(3.1)
![]()
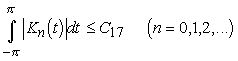 (3.2)
(3.2)
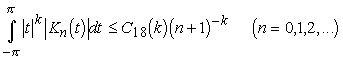 (3.3)
(3.3)
Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.
Категории:
Предыдущая страница реферата | 9 10 11 12 13 14 15 16 17 18 19 | Следующая страница реферата
 Главная
Главная