Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

Эту лемму можно считать известной. Как показывает простой подсчет, совершенно аналогичный проводившемуся Джексоном, в качестве ядер Kn(t) можно взять ядра Джексона достаточно высокой степени, то есть положить

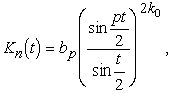
где k0-целое, не зависит от n, натуральное p определяется из неравенства

,

а bp выбираются так, чтобы была выполнена нормировка (3.1).

Лемма 8. Если последовательность ядер {Kn(t)} удовлетворяет всем условиям предыдущей леммы, то

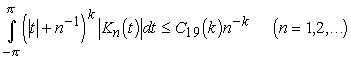(3.4)

Доказательство. Имеем, пользуясь (3.2) и (3.3)

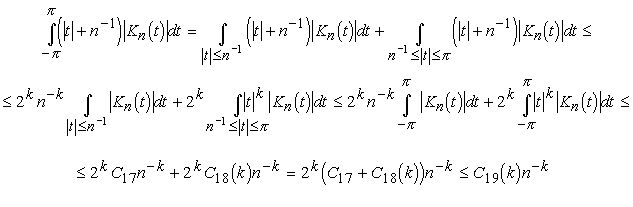
Лемма доказана.

Теорема 1. Пусть k-натуральное число. Тогда

(3.5)

Доказательство. Пусть последовательность ядер {Kn(t)} (n=1,1,2,...) удовлетворяет всем условиям леммы 7. Положим

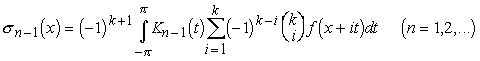
Очевидно, есть тригонометрический полином порядка не выше n-1. Оценим Имеем

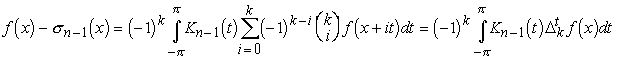
Поэтому

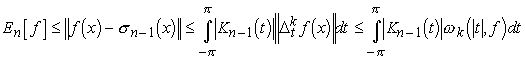(3.6)

Оценим последний интеграл. Полагая в неравенстве (2.6) 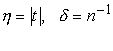, получим, что

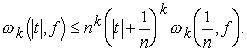
Отсюда и из (3.4) следует:

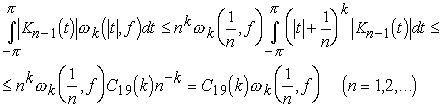
Подставляя эту оценку в (3.6), получаем утверждение теоремы. Теорема доказана.

Следствие 1.1. Пусть k-натуральное число, r-целое неотрицательное. Тогда

(3.7)

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.





Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата