Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

 

а а2 в зависимости от знаков f(a), f(b), f(a1), если f(a)<0, f(b)>0,

 , f(a1)<0

 , f(a1)>0

Если случайно окажется, что точка а3, вычисленная по формуле (1.9), лежит за пределами отрезка [a, b], то на следующем шаге надо вместо этой точки взять ближайший к ней конец этого отрезка (рис. 1.9, б). Оказывается, что сходимость усовершенствованного метода хорд гораздо быстрее, чем у обычного. Именно, если x - корень уравнения f(x)=0, то:

|an+ 1|<C×|an-x| S, где  

10. Комбинированный метод решения уравнений

При решении уравнений часто комбинируют методы хорд и Ньютона. Если график функции y=f(x) обращён вогнутостью вверх, то находят точки а1 и х1 по формулам:

 (1.10)

 (2.10)

Если же график функции y=f(x) обращён вогнутостью вниз, то точку а1 находят по формуле (1.10), а точку х1 – по формуле: 

 (3.10)

Как видно из рис.1.10 а) и б), корень x уравнения f(x)=0 лежит обычно между полученными точками а1 и х1. Применяя снова к этим точкам формулы метода хорд и метода Ньютона, получают новую пару точек а2 и х2 и т. д.

Таким путём получают две последовательности точек а1, а2, а3, …, an, … и x1, x2, x3, … , xn, …, приближаются с разных сторон к искомому корню x. Преимущество описанного метода состоит в том, что при нём получаются приближённые значения как с избытком так и с достатком.

рис.1.10

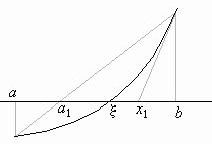
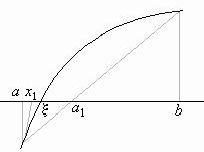
а) б)

11. Заключительные замечания

Ситуация, когда одну и ту же задачу можно решить многими способами, является довольно типичной. В таких случаях естественно возникает необходимость сравнения их между собой.

При оценке эффективности численных методов существенное значение имеют различные свойства:

универсальность;

простота организации вычислительного процесса и контроля над точностью;

скорость сходимости.

Наиболее универсальным является метод деления пополам (дихотомии): он только требует непрерывности функции. Остальные методы накладывают более сильные ограничения. Во многих случаях это преимущество метода вилки может оказаться существенным.

С точки зрения организации вычислительного процесса все виды численного нахождения корней уравнения очень просты. Однако и здесь метод деления пополам обладает некоторым преимуществом. Вычисления можно начинать с любого отрезка [a, b], на концах которого непрерывная функция f(x) принимает значения разных знаков. Процесс будет сходится к корню уравнения f(x)=0, причём на каждом шаге он даёт для корня двустороннюю оценку, по которой легко определить достигнутую точность. Сходимость же метода итераций или касательных зависит от того, насколько удачно выбрано нулевое приближение.

Рекомендуем скачать другие рефераты по теме: диплом вуза, стратегия реферат.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата