|
2 |
|
4,6 — 5,5 |
4 |
|
5,5 — 6,4 |
6 |
|
6,4 — 7,3 |
5 |
|
7,3 — 8,2 |
3 |
|
Итого |
20 |
Мода (Мо) — наиболее часто встречающееся значение признака в совокупности — для данного ряда распределения. В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться только мода или медиана. Для определения их величины используются следующие формулы:
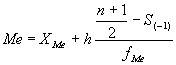
где ХMe — нижняя граница медианного интервала;
h — величина интервала;
S(-1) — накопленная частота интервала, предшествующего медианному;
fMe — частота медианного интервала.
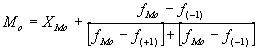
где Х — начало модального интервала;
fMo — частота, соответствующая модальному интервалу;
f(-1) — предмодальная частота;
f(+1) — послемодальная частота.
Используя данные примера, приведенные в таблице 3, рассчитаем медиану. По накопленным частотам определяем, что медиана находится в интервале 5,5 — 6,4. Тогда
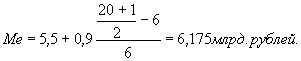
Таким образом, 50 % банков имеют прибыль менее 6,175 млрд. руб, а 50 % банков более 6,175 млд. руб.
Наибольшая частота соответствует также интервалу 5,5 — 6,4, т.е. мода должна находится в этом интервале. Приведенная формула моды может быть использована в вариационных рядах с равными интервалами.
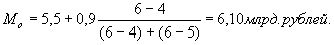
Таким образом, в данной совокупности наиболее часто встречается размер прибыли 6,10 млрд. руб.
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ, ЕЕ СВОЙСТВА И ДРУГИЕ СТЕПЕННЫЕ СРЕДНИЕ.
Рекомендуем скачать другие рефераты по теме: баллов рефераты, налоговая реферат.
Предыдущая страница реферата |
5
6
7
8
9
10
11
12
13
14
15 |
Следующая страница реферата
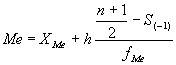
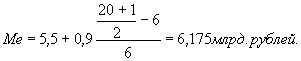
 Главная
Главная