Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15

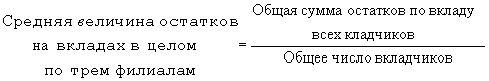
После того как записана логическая формула средней, которую нужно вычислить, необходимо внимательно рассмотреть имеющиеся для вычисления данные и заменить словесные обозначения числителя и знаменателя логической формулы средней соответствующими цифровыми данными, после чего остается только провести необходимые вычисления.

Этот принцип обеспечивает правильный выбор формы средней, а, следовательно, и правильное определение величины средней. И еще одно важное свойство принципа логической формулы в том, что здесь не возникает проблема выбора весов средней.

При применении средней геометрической индивидуальные значения признака представляют собой, как правило, относительные величины динамики, и построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики (причем временные отрезки ряда динамики одинаковы). Средняя характеризует, таким образом, средний коэффициент роста.

Средняя геометрическая величина используется также для определения равноудаленной величины от максимального и минимального значений признака.

Формула средней квадратической используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения. Так, при расчете показателей вариации среднюю вычисляют из квадратов отклонений индивидуальных значений признака от средней арифметической величины.

 

Список использованной литературы

Общая теория статистики, А.А. Спирин, О.Э Башина

Общая теория статистики, Ефимова М.Р., Петрова Е.В., Румянцев В. Н.

Общая теория статистики, Овсиенко В. Е .

Теория статистики, П.А. Шмойлова

Скачали данный реферат: Горбачёв, Sokrat, Filippin, Яресько, Nikitaev, Begichev.
Последние просмотренные рефераты на тему: реферат туризм, конспекты 9 класс, рецензия на дипломную работу образец, сочинение капитанская.





Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15