Claw.ru | Рефераты по математике | Производная и ее применение в алгебре, геометрии, физике Производная и ее применение в алгебре, геометрии, физике | Категория реферата: Рефераты по математике | Теги реферата: новейшие рефераты, ресурсы реферат | Добавил(а) на сайт: Янборисов. Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата	Данная функция
1	- ∞ < x< - 4/3	—	—	+	возрастает
2	-4/3 < x < 2	+	—	—	убывает
3	2 < х < + ∞	+	+	+	возрастает

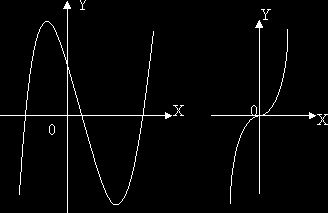Следовательно, данная функция возрастает в промежутках

- ∞ <x < -4/3 и 2 <x < + ∞ и убывает в промежутке — 4/3 < х <2.

График данной функции представлен на черт.

5°.Функция у = х3 (черт.) имеет производную у = 3х2, которая положительна при всяком значении х, отличном от нуля. При х = 0 производная у' = 0. Функция у = х3 возрастает в промежутке — ∞<x<+∞; x= 0 есть отдельная единственная точка, в которой производная равна нулю, в ней функция возрастает. Действительно, при х = 0 х3 = 0, а при х < 0 х3 < 0 и при х > 0 х3 > 0.

Задачи на отыскание наибольших и наименьших значений величин

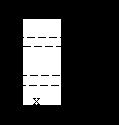1°. Требуется огородить проволочной сеткой длиной 60 м прямоугольный участок, прилегающий к стене дома ( черт.). Каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь?

Рекомендуем скачать другие рефераты по теме: греция реферат, республика реферат.





Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата