Claw.ru | Рефераты по математике | Производная и ее применение в алгебре, геометрии, физике Производная и ее применение в алгебре, геометрии, физике | Категория реферата: Рефераты по математике | Теги реферата: новейшие рефераты, ресурсы реферат | Добавил(а) на сайт: Янборисов. Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата

25

→∞

Следовательно, периметр прямоугольника имеет наименьшее значение (минимум), если длина его 6 м и ширина 36/6 м = 6 м, т. е. когда он квадрат.

Максимум и минимум функции

Задачи на отыскание наибольших и наименьших значений величин имеют важное значение в технике и, как это ясно из примеров, сводятся к отысканию максимума и минимума функции.

Определение. 1. Функция f(x) имеет при х=с максимум, если ее значение при х=с больше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с.

2. Функция f(x) имеет при x= с минимум, если ее значение при х=с меньше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с.

Термины "максимум" и "минимум" объединяются в один общий для них термин "экстремум".

Значение аргумента, которое дает максимум (или минимум) функции, называется точкой максимума (минимума), или точкой экстремума.

Функция может иметь только максимум, например функция y = 60x— 2х2 (черт. 111), или только минимум, например функция у = 2х+72/x (черт. 112), или иметь

максимум и минимум, как, например, функция у = х3— — х2 — 8х+2 (черт. 108). Функция может иметь несколько максимумов и минимумов (черт. 113), причем в этом случае максимумы и минимумы чередуются. Функция может не иметь ни максимума, ни минимума. Например, функции у = х3, y = ctgx, y = ax не имеют ни максимума, ни минимума, так как при возрастании х от — ∞ до +∞ первая и третья функции возрастают, а вторая только убывает.

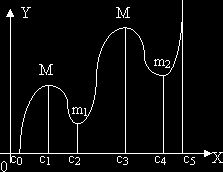
Максимум (минимум) функции может не быть наибольшим (наименьшим) значением ее. Так, изображенная на черт. 113 функция имеет в точке с. значение, большее максимумов с1М1 и с3М2, а в точке с0 значение, меньшее минимума c2m1, и c4m2, минимум c4m2 больше максимума с1М1. Максимум (минимум) функции в данной точке вообще есть наибольшее (наименьшее) значение функции по сравнению с ее значениями в точках, лежащих слева и справа от точки экстремума лишь в достаточной близости к ней.

Признаки существования экстремума

1°. Теорема (необходимый признак). Если в окрестности 2δ точки х=с:

1) функция f(х) дифференцируема, 2) значение х=с есть точка экстремума функции f(x), то ее производная в точке с равна нулю, m. e. f '(c) = 0.

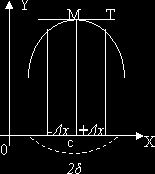
Доказательство. Пусть для определенности х=c есть точка максимума (черт. 111). Представим значения независимого переменного х левой полуокрестности точки с в виде с — Δx:, а правой в виде с+ Δx, где 0< Δx < δ. Значение функции f(x) в точке с есть f(c), в левой полуокрестности оно равно f(с — Δx), а в правой f(c + Δx). Значения f(x) в окрестности 2δ точки с поставлены, таким образом, в зависимость от значений Δx, причем значение х = с -/+ Δx неограниченно приближается к числу с, если Δx стремится к нулю.

По определению максимума функции:

f(c- Δx)<f(c) и f(c + Δx)<f(c).

Отсюда:

f(c-Δx)-f(c)<0 и f(c + Δx)-f(с)<0.

Левые части неравенств выражают приращение функции в точке х = с при изменении аргумента соответственно на — Δx и + Δx. Составив отношение приращения функции к приращению аргумента, получаем:

lim ((f(c - Δx)-f(c))/(—Δx)) = f‘(c)  и  lim ((f(c + Δx)-f(c))/(+Δx)) = f‘(c).  - Δx→0                                                                 + Δx→0

(f(c —Δx)—f(с))/(-Δx))>0 (1); (f(с + Δx)—f(с)/(+Δx))<0 (2) Оба отношения (1) и (2) имеют один и тот же предел при Δx → 0, так как по условно функция f(x) имеет в точке с определенную произвольную:

Из неравенства (1) следует, что f '(с) либо положительна, либо равна нулю, а неравенство (2) показывает, что f '(с) не может быть положительной. Следовательно,

f‘(c) = 0,

что и требовалось доказать.

Рекомендуем скачать другие рефераты по теме: греция реферат, республика реферат.





Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата