Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Доказательство. На прямой (AB) можно легко найти две точки O и C, принадлежащие множеству F (одна из них будет внутренней точкой отрезка [AB], другая - внешней точкой этого отрезка). Рассмотрим инверсию относительно окружности с центром в точке O произвольного радиуса R. Для образов точек A, B и C имеем

   |C¢A¢|

|C¢B¢|      =          |CA|R2/(|OC|·|OA|)

|CB|R2/(|OC|·|OB|)         =          |CA|

|CB|        :           |OA|

|OB|      = k:k = 1. 1

Пусть X¢ = invOR(X) и F¢ = invOR(F). Тогда, учитывая (1) и сохранение при инверсии отношения четырех точек, получаем

X Î FÛ            |XA|

|XB|        :           |CA|

|CB|          = k:k = 1Û

Û          |X¢A¢|

|X¢B¢|      :           |C¢A¢|

|C¢B¢|      = 1Û   |X¢A¢|

|X¢B¢|                 = 1.

Последнее означает, что F¢ - серединный перпендикуляр к отрезку [A¢B¢]. Отсюда F = invOR(F¢) - окружность, диаметр которой лежит на прямой (AB).

Формула следующей теоремы, названная в честь Леонарда Эйлера6, связывает между собой радиусы вписанной и описанной окружностей произвольного треугольника с расстоянием между их центрами.

Теорема. Пусть для произвольного треугольника ABC числа r, R и d соответственно обозначают радиусы вписанной и описанной окружностей и расстояние между их центрами. Тогда d2 = R2-2Rr.

Доказательство. Точки касания вписанной окружности w(O,r) со сторонами [AB], [AC] и [BC] обозначим соответственно через K, L и M (рис. 11).

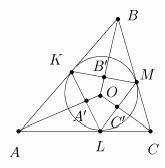
Рис. 11

Пусть также w1(O1,R) - описанная около треугольника DABC окружность. Рассмотрим инверсию относительно вписанной окружности w(O,r). Так как прямые (AK) и (AL) являются касательными к окружности инверсии, образом точки A будет середина отрезка [KL] (точка A¢), аналогично B¢ = invOr (B) - середина [KM] и C¢ = invOr (C) - середина [LM]. Образом окружности w1(O1,R) будет окружность w1¢, проходящая через точки A¢,B¢,C¢ и имеющая радиус равный r/2 (так как при гомотетии HO-1/2 окружность w переходит в окружность, проходящую через середины сторон DKLM, т.е. в w1¢). Теперь попробуем выяснить, как вообще изменяется радиус окружности при инверсии. Обозначим через X и Y точки диаметра окружности w1(O1,R), лежащие на прямой (OO1) (рис. 12).

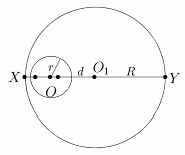
Рис. 12

По свойству IX отрезок [invOr(X) invOr (Y)] является диаметром окружности

invOr (w1), а по свойству V его длина равна

Рекомендуем скачать другие рефераты по теме: реферат россия скачать, пример реферата.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата