
Теория цепных дробей
| Категория реферата: Рефераты по математике
| Теги реферата: реферат суды, доклад
| Добавил(а) на сайт: Разуваев.
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16 | Следующая страница реферата
3
Очевидно, нам достаточно взять Решенные задачи в более общем виде формулируются так: Найти рациональное приближение к действительному со знаменателем
со знаменателем 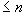 в виде наиболее близкой к в виде наиболее близкой к  подходящей дроби. Для этого надо взять подходящую дробь для
подходящей дроби. Для этого надо взять подходящую дробь для  с наибольшим знаменателем, не превышающим n.
Найти рациональное приближение к действительному числу
с наибольшим знаменателем, не превышающим n.
Найти рациональное приближение к действительному числу  с возможно меньшим знаменателем так, чтобы погрешность не превосходила
с возможно меньшим знаменателем так, чтобы погрешность не превосходила 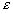 (то есть с точностью до
(то есть с точностью до 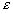 ). Для этого, пользуясь аппаратом
цепных дробей, находим подходящую дробь ). Для этого, пользуясь аппаратом
цепных дробей, находим подходящую дробь 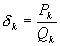 с наименьшим
знаменателем с наименьшим
знаменателем 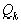 так, чтобы так, чтобы 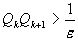 .
2.3. Теорема Дирихле. .
2.3. Теорема Дирихле.
Выше мы нашли оценку погрешности, возникающей при замене любого действительного числа А сейчас рассмотрим некоторые сравнительно простые результаты, показывающие как обстоит дело с приближением действительных чисел рациональными числами, не предрешая заранее, что эти рациональные числа будут подходящими дробями. Пусть Например, можно поставить задачу нахождения такого рационального приближения к Теорема Дирихле: Пусть (или: существует такая пара взаимно простых целых чисел a и b, что Доказательство: Теорему легко доказать с помощью аппарата цепных дробей. Пусть 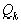 не является последним знаменателем, то есть существует не является последним знаменателем, то есть существует 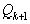 такое, что такое, что 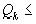 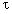 < <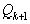 . Тогда при a= . Тогда при a=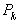 и b= и b=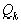 имеем:
имеем:
2)
Теорема доказана. Сам Дирихле дал другое доказательство, использовав в нем принцип, который носит теперь имя Дирихле: при распределении N объектов между N-1 ящиками хотя бы в одном ящике должно находиться 2 объекта. Приведем это доказательство. Пусть 
Так как чисел у нас t+2, то (согласно принципу Дирихле) обязательно найдется такой промежуток, который содержит 2 числа из совокупности 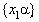 и и 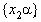 , то , то 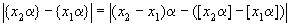 . Пусть . Пусть 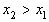 и и 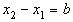 , , 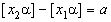 . Так как . Так как 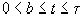 , то , то 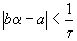 , , 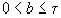 ).
Если ).
Если 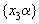 и 1 принадлежат одному промежутку, то и 1 принадлежат одному промежутку, то
Пусть в таком случае Теорема доказана. Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7. Категории:Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|