
Теория цепных дробей
| Категория реферата: Рефераты по математике
| Теги реферата: реферат суды, доклад
| Добавил(а) на сайт: Разуваев.
Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата
Доказательство: Из формулы (5) следует
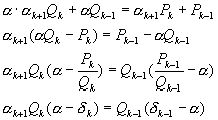
Но 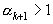 ,
, 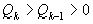 , так что
, так что 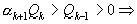
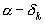 ) и (
) и (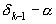 ) имеют одинаковый
знак, а это значит, что
) имеют одинаковый
знак, а это значит, что  находится между
находится между 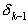 и
и 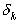 ;
;
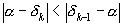 , то есть
, то есть  ближе к
ближе к 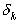 ,
чем к
,
чем к 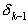 .
.
Теорема доказана.
Так как 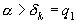 , то
, то 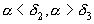 , и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
, и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
 больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального
больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального 
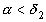
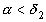 указанные последовательности являются бесконечными), то есть
указанные последовательности являются бесконечными), то есть
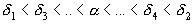
(в случае рационального 
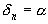 ).
).

Учитывая то, что при 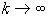
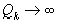 , вследствие чего
, вследствие чего 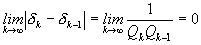 , переходим к дальнейшему выводу, что в случае иррационального
, переходим к дальнейшему выводу, что в случае иррационального  сегменты
сегменты 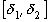 ,
, 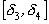 , … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей
, … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей 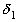 ,
, 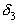 , … и
, … и 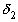 ,
, 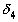 , … . Но так как
, … . Но так как  принадлежит всем сегментам последовательности, то
принадлежит всем сегментам последовательности, то  и совпадает с указанной точкой, так что
и совпадает с указанной точкой, так что 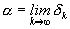 .
.
Итак, мы имеем следующий важный результат:
бесконечная последовательность подходящих дробей 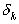 , которая возникает при разложении иррационального
, которая возникает при разложении иррационального  , сходится к
, сходится к  , колеблясь около него. Или: иррациональное действительное
, колеблясь около него. Или: иррациональное действительное  равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
Теперь покажем, что сходящейся является последовательность подходящих дробей не только такой бесконечной непрерывной дроби, которая возникает при разложении иррационального числа  , но и любой бесконечной непрерывной дроби
, но и любой бесконечной непрерывной дроби 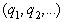 , где
, где 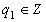 , а
, а 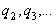 - произвольно выбранные целые положительные числа.
- произвольно выбранные целые положительные числа.
Но для этого мы заново исследуем взаимное расположение подходящих дробей.
С этой целью рассмотрим формулы:
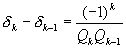 (1) и
(1) и 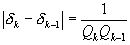 (2),
(2),
которые справедливы для любой бесконечной непрерывной дроби.
Формула (1) показывает, что любая подходящая дробь четного порядка больше двух соседних подходящих дробей, у которых порядок на единицу меньше или больше, чем у нее, то есть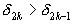 и
и 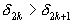 . Согласно
этому
. Согласно
этому 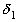 и
и 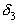 расположены слева
от
расположены слева
от 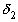 ,
, 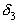 и
и 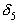 – слева от
– слева от 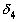 и так далее.
Формула (2) показывает, что расстояние между соседними подходящими дробями
при увеличении k убывает. Действительно, так как
и так далее.
Формула (2) показывает, что расстояние между соседними подходящими дробями
при увеличении k убывает. Действительно, так как 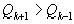 ,
то
,
то
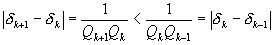
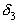 ближе к
ближе к 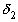 ,
чем
,
чем 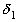 , а так как
, а так как 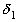 и
и 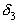 находятся слева от
находятся слева от 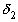 , то
, то 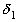 <
<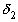 .
.

Из этого следует, что подходящая дробь 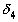 , которая, как и
, которая, как и 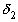 , расположена справа от
, расположена справа от 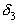 , ближе к
, ближе к 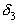 , чем к
, чем к 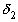 , то есть
, то есть 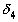 <
<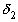 .
.
Подходящие дроби дальнейших порядков располагаются таким же образом.
Итак, подходящие дроби нечетного порядка увеличиваются с ростом порядка, а подходящие дроби четного порядка убывают с ростом порядка; при этом все подходящие дроби нечетного порядка меньше всех подходящих дробей четного порядка, то есть 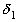 <
<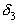 <…<
<…<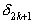 <…<
<…<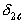 <…<
<…<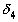 <
<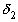 при любых k и
при любых k и 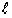 .
.
Так как 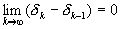 , то пары подходящих дробей
, то пары подходящих дробей 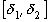 ,
, 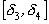 , … образуют стягивающуюся последовательность отрезков, которая должна иметь единственную общую точку, являющуюся общим пределом последовательностей
, … образуют стягивающуюся последовательность отрезков, которая должна иметь единственную общую точку, являющуюся общим пределом последовательностей 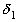 ,
, 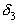 , … и
, … и 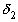 ,
, 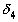 , …. Обозначим этот предел за
, …. Обозначим этот предел за  , имеем
, имеем 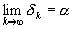 , причем, очевидно,
, причем, очевидно, 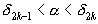 для любого k, то есть
для любого k, то есть  находится между любыми двумя соседними подходящими дробями.
находится между любыми двумя соседними подходящими дробями.
Следовательно, подходящие дроби любой бесконечной непрерывной дроби имеют некоторый предел  . Этот предел
. Этот предел  принимается в качестве значения бесконечной непрерывной дроби. Говорят, что бесконечная непрерывная дробь сходится к
принимается в качестве значения бесконечной непрерывной дроби. Говорят, что бесконечная непрерывная дробь сходится к  или представляет число
или представляет число  . Можно записать
. Можно записать  =
=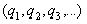 , подразумевая при этом, что
, подразумевая при этом, что  =
=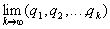 .
.
Исходя из результатов, которые мы получили выше, можно утверждать, что для каждого действительного иррационального  существует представление в виде бесконечной непрерывной дроби. Таким представлением является разложение
существует представление в виде бесконечной непрерывной дроби. Таким представлением является разложение  в бесконечную непрерывную дробь, так как предел подходящих дробей последней равен как раз
в бесконечную непрерывную дробь, так как предел подходящих дробей последней равен как раз  .
.
Возникает вопрос, сколько представлений действительного иррационального  в виде бесконечных непрерывных дробей существует вообще? Покажем, что только одно.
в виде бесконечных непрерывных дробей существует вообще? Покажем, что только одно.
Другими словами: представление действительного иррационального  в виде бесконечной непрерывной дроби всегда является разложением
в виде бесконечной непрерывной дроби всегда является разложением  с помощью выделения целой части. Докажем это важное утверждение.
с помощью выделения целой части. Докажем это важное утверждение.
Пусть действительное иррациональное  представлено бесконечной непрерывной дробью
представлено бесконечной непрерывной дробью 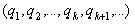 , то есть
, то есть  =
=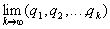 . Назовем бесконечную непрерывную дробь
. Назовем бесконечную непрерывную дробь 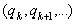 остатком данной дроби порядка k. Так как любая бесконечная непрерывная дробь представляет некоторое действительное число, то это утверждение относится также и к остатку
остатком данной дроби порядка k. Так как любая бесконечная непрерывная дробь представляет некоторое действительное число, то это утверждение относится также и к остатку 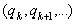 . Обозначим его через
. Обозначим его через 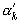 ,
, 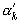 =
=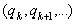 , то есть
, то есть 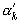 =
=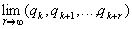 . Аналогично
. Аналогично 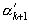 =
=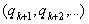 , то есть
, то есть 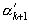 =
=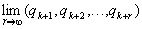 .
.
Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.
Категории:
Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата
 Главная
Главная