
Теория цепных дробей
| Категория реферата: Рефераты по математике
| Теги реферата: реферат суды, доклад
| Добавил(а) на сайт: Разуваев.
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16 | Следующая страница реферата
Округляя десятичное выражение действительного
 до n–го знака после запятой, мы тем самым представляем
до n–го знака после запятой, мы тем самым представляем  приближенно дробью
приближенно дробью 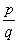 со знаменателем
со знаменателем 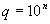 , причем погрешность
, причем погрешность 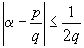 , если же
, если же 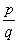 подходящая дробь к
подходящая дробь к  , то
, то 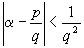 , так что при сколько-нибудь значительном q величина
, так что при сколько-нибудь значительном q величина 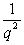 во много раз меньше, чем
во много раз меньше, чем 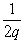 .
.
Пример: Десятичное выражение числа 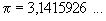 в виде рациональной дроби со знаменателем
в виде рациональной дроби со знаменателем 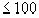 имеет вид
имеет вид 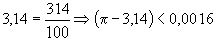 . Если же
. Если же 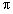 разложить в цепную дробь, получается
разложить в цепную дробь, получается 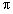 =(3, 7, 15, …);
=(3, 7, 15, …); 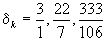
Наибольшей подходящей дробью для 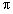 со знаменателем
со знаменателем 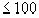 является число
является число 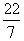 , известное уже Архимеду, причем
, известное уже Архимеду, причем 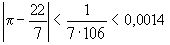 . Итак, мы получили, что приближение подходящей дробью дает большую точность, чем приближение десятичной дробью.
. Итак, мы получили, что приближение подходящей дробью дает большую точность, чем приближение десятичной дробью.
Это объясняется тем, что знаменатели подходящих дробей определяются арифметической природой изображаемого числа, а знаменатели же приближающих десятичных дробей не могут быть иными, как только 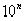 .
.
Теорема: Если рациональное число 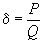 ближе к действительному числу
ближе к действительному числу  , чем его подходящая дробь
, чем его подходящая дробь 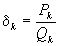 , где k>1, то
, где k>1, то 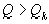 , то есть если
, то есть если 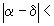
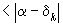 , то
, то 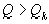 .
.
Доказательство: Рассмотрим случай, когда 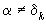 (иначе теряет смысл). Тогда
(иначе теряет смысл). Тогда  всегда лежит между любыми двумя последующими подходящими дробями так, что для k>1
всегда лежит между любыми двумя последующими подходящими дробями так, что для k>1  всегда лежит между
всегда лежит между 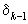 и
и 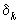 , причем ближе к
, причем ближе к 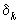 , чем к
, чем к 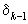 . Поэтому, если
. Поэтому, если 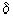 ближе к
ближе к  , чем
, чем 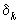 , то оно находится между
, то оно находится между 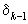 и
и 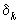 . В случае четного
. В случае четного 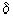 можно записать
можно записать 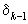 <
<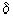 <
<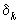 (в случае нечетного k доказательство существенно не меняется), откуда
(в случае нечетного k доказательство существенно не меняется), откуда 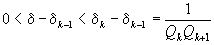 , или
, или 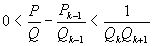
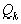
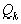 ,
, 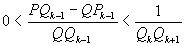 , откуда, домножая неравенство на
, откуда, домножая неравенство на 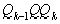 , получаем
, получаем 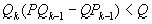 . Так как
. Так как 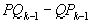 – число целое и положительное, то из предыдущего равенства следует
– число целое и положительное, то из предыдущего равенства следует 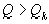 , что и требовалось доказать.
, что и требовалось доказать.
Попутно мы установили, что любая рациональная дробь 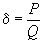 , принадлежащая интервалу
, принадлежащая интервалу 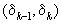 , k>1, имеет знаменатель
, k>1, имеет знаменатель 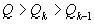 . Для k=1 теорема неверна:
. Для k=1 теорема неверна:
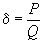 может оказаться ближе к
может оказаться ближе к  , чем его подходящая дробь
, чем его подходящая дробь 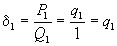 , хотя
, хотя 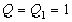 .
.
Доказанная теорема приводит нас к следующему определению:
Рациональную дробь 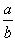 называют наилучшим приближением действительного
называют наилучшим приближением действительного  , если любая более близкая к
, если любая более близкая к  рациональная дробь
рациональная дробь 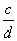 имеет больший знаменатель, чем
имеет больший знаменатель, чем 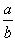 , то есть если из
, то есть если из 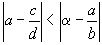 следует d>b.
следует d>b.
Таким образом, подходящие дроби являются наилучшими приближениями, например, Архимедово число 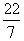 для
для 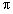 является наилучшим приближением.
является наилучшим приближением.
Ранее мы доказали, что для оценки погрешности 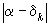 , возникающей при замене любого действительного
, возникающей при замене любого действительного  его подходящей дробью
его подходящей дробью 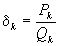 , можно пользоваться неравенством
, можно пользоваться неравенством 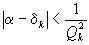 . Выразим этот результат по отношению к действительному иррациональному
. Выразим этот результат по отношению к действительному иррациональному  , имеющим бесконечное множество подходящих дробей, следующим образом: для любого действительного иррационального
, имеющим бесконечное множество подходящих дробей, следующим образом: для любого действительного иррационального  существует при c=1 бесконечное множество несократимых дробей
существует при c=1 бесконечное множество несократимых дробей 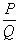 таких, что
таких, что 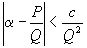 (1).
(1).
Такими дробями являются, например, все подходящие дроби для 
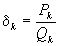 .
.
Возникает вопрос: При каких меньших значениях c (чем c=1) существует для любого действительного иррационального  бесконечное множество (несократимых) рациональных приближений
бесконечное множество (несократимых) рациональных приближений 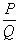 , погрешность которых
, погрешность которых 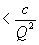 .
.
Теорема: Для любого действительного иррационального числа  существует при
существует при 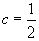 бесконечное множество несократимых рациональных дробей
бесконечное множество несократимых рациональных дробей 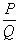 таких, что
таких, что 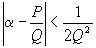 (
(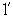 ). Такими рациональными дробями могут быть только подходящие дроби к
). Такими рациональными дробями могут быть только подходящие дроби к  .
.
Доказательство: Докажем первую часть теоремы. Рассмотрим две последующие подходящие дроби к 
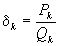 и
и 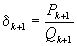 . Допустим, что ни одна из этих дробей не удовлетворяет неравенству (
. Допустим, что ни одна из этих дробей не удовлетворяет неравенству (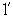 ). Тогда имеем:
). Тогда имеем: 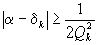 ,
, 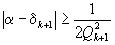 . Отсюда
. Отсюда 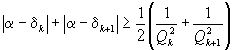 .
.
Но так как  лежит между
лежит между 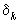 и
и 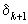 , то
, то 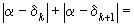
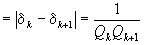 , вследствие чего
, вследствие чего 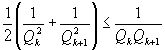 , или
, или 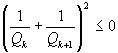 , а это для k>1 невозможно. Мы пришли к противоречию, значит наше допущение неверно, а верно то, что требуется доказать.
, а это для k>1 невозможно. Мы пришли к противоречию, значит наше допущение неверно, а верно то, что требуется доказать.
Для доказательства второй части теоремы докажем достаточный признак подходящей дроби к действительному числу  : если
: если 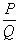 , где Q>0, несократимая дробь и для действительного
, где Q>0, несократимая дробь и для действительного  имеет место неравенство (
имеет место неравенство (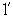 ), то
), то 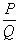 является подходящей дробью к
является подходящей дробью к  .
.
Доказательство: Покажем, что если 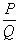 =(
=(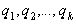 )=
)=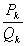 (
(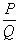 удовлетворяет условию теоремы) подходящая дробь к
удовлетворяет условию теоремы) подходящая дробь к  , то соответствующее остаточное число
, то соответствующее остаточное число 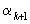 разложения данного
разложения данного  в цепную дробь окажется >1. Действительно,
в цепную дробь окажется >1. Действительно, 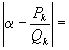
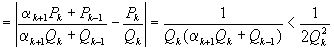 , откуда следует
, откуда следует 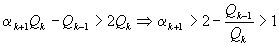 , так как
, так как 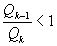 .
.
Теорема доказана полностью.
Достаточный признак подходящей дроби не является ее необходимым признаком; могут существовать подходящие дроби для  , которые ему не удовлетворяют.
, которые ему не удовлетворяют.
Крайнюю возможность уменьшения c в указанном раньше смысле выражает теорема Гурвица-Бореля:
Теорема: Для любого действительного иррационального числа  существует при
существует при 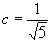 бесконечное множество несократимых рациональных дробей
бесконечное множество несократимых рациональных дробей 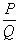 таких, что выполняется неравенство (1), то есть неравенство
таких, что выполняется неравенство (1), то есть неравенство
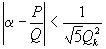 , (
, (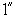 )
)
если же 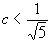 , то существуют такие действительные иррациональные
, то существуют такие действительные иррациональные  , для которых неравенство (1) имеет не более конечного числа рациональных решений
, для которых неравенство (1) имеет не более конечного числа рациональных решений 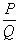 .
.
Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.
Категории:
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16 | Следующая страница реферата
 Главная
Главная