Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

L – фактическая нижняя граница того раздела оценок, который включает себя нужную нам оценку

cumf – накопленная в данной нижней границе частота

f – количество оценок в данном разделе

p – определяемый процентиль (в данном случае 0,25)

p*n = 0,25*125=31,25

Находим фактическую нижнюю границу раздела L, содержащую 31,5 (это между 34 и 16).

Нижняя граница оценки 28,5

L=28,5f=34-16=18

Вычитаем накопленную частоту L из произведения nf: ((31,25-16)/18) + 28,5=29,35

Для определения процентиля в случае наличия интервалов оценок, формула принимает вид:

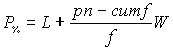
где W – ширина любого интервала оценок (в примере =1).

Наглядное представление данных

В табличных процессорах представляется возможность оформить численные данные в виде графика или диаграммы различного вида, но разновидностей графического представления данных существует больше, чем это предусмотрено программным обеспечением и прежде чем использовать какой-либо из видов необходимо:

выделить в данных существенную информацию; знать все типы представления данных и сделать правильный выбор; знать и грамотно использовать потенциал аудитории, для представления которой готовятся данные; если оформление осуществляется не вами, разработать подробные и четкие инструкции для технического персонала с учетом имеющихся средств.

Примеры диаграмм и графиков: линейная, столбиковая, полосчатая, кумулятивная кривая, данные накапливаются с течением времени, пиктограмма – данные представляются в виде стилизованных изображений (улов рыбы в виде рыбы), логарифмическая диаграмма, круговая диаграмма.

Графическое представление распределения частот Столбиковая диаграмма (гистограмма) Полигон распределения Сглаженная кривая

Гистограмма - это последовательность столбцов, каждый из которых опирается на один раздельный интервал, а высота столбца – это частота или количество случаев.

Принято распределять горизонтальную шкалу на один раздельный интервал вправо и влево от полученного диапазона. Чтобы гистограмма не получилась сплющенной или вытянутой, выбирают такой масштаб шкалы, чтобы ее ширина составляла 1 2/3 высоты. Середина столбца совмещается с срединой интервала, на практике ее изображают в форме контура, опуская вертикальные линии.

Полигон распределения – это та же гистограмма, но линии соединяют середины столбцов каждого разрядного интервала. Так как на разрядах справа и слева от разрядов распределения частот, частота имеет нулевое значение, поэтому полигон распределения продолжают до горизонтальной оси в середине интервала ниже меньшей оценки и выше высшей оценки.

Огива производится по точкам максимально приближенно без углов или острых фигур, ее называют кривой процентелей. Точки, определяющие кривую процентелей расположены по горизонтали у верхней границы каждого раздела. Огива проходит путь от 0 до 100%. При рисовании огивы надо следить за тем (особенно при малом числе объектов), чтобы, когда мы сглаживаем кривую, над ней оставались бы столько же точек, сколько и под ней. При отсутствии любых графических средств можно создать гистограмму на пишущей машинке в виде полосчатой диаграммы.

Гистограмма наиболее легка для восприятия и используется в тех случаях когда всего одно распределение. Если надо сравнить два и более распределений, используют полигон, чтобы избежать запутанной картины.

Огива дает возможность оценить квантили, медианы и другие характеристики точки. Удобно сравнивать несколько групп данных на одном графике.

Ошибки при использовании графиков при создании графика не определяли положение нулевой точки; представили значения в виде площадей в том случае, когда их надо было отражать линейно; при использовании небольшого количества объектов сделали вывод относительно всей совокупности. Правила графического оформления Вся структура графика предполагает его чтение слева на право, вертикальные шкалы – снизу вверх; На вертикальной шкале разместить нулевую отметку; Если нулевая линия вертикальной шкалы не перпендикулярна по отношению к графику, то нулевая линия должна быть показана с помощью горизонтальной оси. Пороговые точки на шкалах желательно выделить размером или цветом, но если речь идет о временном интервале, предпочтительно не указывать начальной и конечной точек. Подобрать такой масштаб, чтобы кривые линии резко отличались от прямых, желательно включить в график цифровые данные и изображение формулы, расположив их в правом верхнем углу, при необходимости использовать ясные полные заголовки и подзаголовки, как для самой диаграммы, так и для ее осей. Меры центральной тенденции – первый момент, характеризующие данные

При исследовании массивов данных мы чаще всего оперируем величинами, характеризующими этот массив, именно по ним делаем вывод обо всей совокупности данных. К таким характеристикам относятся меры центральной тенденции, то есть значение наиболее часто встречающееся в данной совокупности. Этих мер существует несколько:

мода – это такое значение во множестве наблюдений которое встречается наиболее часто. Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9). Соглашения по поводу меры Если все значения в группе встречаются одинокого часто, считают, что у данной группы, моды нет. Когда два соседних значения имеют одинаковую частоту и эти частоты больше любых других частот в группе, то модой считают среднее от этих двух значений. Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этой группы есть две моды, такая группа называется бимодальной. Бимодальной называется группа и в том случае, если эти две черты не совсем равны. В таких случаях договорились различать большую и малую моду и во всей группе, наряду с одной большой модой может быть несколько меньших мод.

медиана – это 50-тый процентиль в группе данных.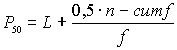

среднее (среднеарифметическое или выборочное среднее) – это сумма всех значений, разделенная на их количество. .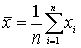

Мода наиболее просто вычисляется и при большом количестве измерений достаточно стабильна и близка к медиане и среднему. Медиана вычисляется по сложнее, особенно легко при ранжированных данных. В больших массивах предлагается сначала сгруппировать их, а потом вычислять медиану. Для определения моды и медианы не требуется знание всех остальных значений.

На определение среднего влияют значения всех изменений.

При наличии интервалов в значении, формула для среднего принимает вид:

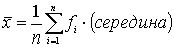Свойства среднего

Рекомендуем скачать другие рефераты по теме: математика, ответ 2.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата