Эти четыре момента составляют набор особенностей распределения при анализе данных.
Нормальное распределение
Нормальное распределение лучше всего описывается кривой созданной ДеМуавром по следующей формуле:
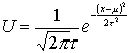
где U – высота кривой над осью x, t
и μ – числа, которые определяют положение кривой относительно числовой оси и регулируют ее размах. Для μ=0, t
=1 график принимает вид:
Эта кривая при μ=0, t
=1 получила статус стандарта, ее называют единичной нормальной кривой, то есть любые собранные данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой. Созданы статистические таблицы со значениями площади под единичной нормальной кривой влево от любой точки на оси z в (-3; 3). Общая площадь под кривой равна 1. И все остальные площади рассматривают как процент от целого.
Свойства нормальных кривых:
Семейство нормальных кривых включают в себе все кривые, которые можно получить по данной формуле, отличающиеся друг от друга только парой значений t
и μ .
1. 68% площади лежит в интервале 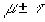
2. 95% площади лежит в интервале 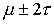
3. 99,7% площади лежит в интервале 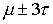
Если x имеет нормальное распределение со средним μ и стандартным отклонение t
, то z равное 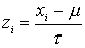 характеризуется распределением со средним равным нулю и стандартным отклонением равным 1. Площадь между двумя значениями x в нормальном распределении равна площади между ux стандартизованными величинами в единичном нормальном распределении. Нормализованную кривую изобрели для решения задач теории вероятности, но оказалось на практике, что она отлично аппроксимирует распределение черт при большом числе наблюдений для множества переменных. Можно предположить, сто не имея материальных ограничений на количество объектов и время проведения эксперимента, статистическое исследование приводило к нормально кривой.
характеризуется распределением со средним равным нулю и стандартным отклонением равным 1. Площадь между двумя значениями x в нормальном распределении равна площади между ux стандартизованными величинами в единичном нормальном распределении. Нормализованную кривую изобрели для решения задач теории вероятности, но оказалось на практике, что она отлично аппроксимирует распределение черт при большом числе наблюдений для множества переменных. Можно предположить, сто не имея материальных ограничений на количество объектов и время проведения эксперимента, статистическое исследование приводило к нормально кривой.
Двумерное нормальное распределение
Если при исследовании появляется вопрос о связи между двумя переменными для одного и того же объекта (например, рост и интеллект) мы говорим о двумерных связях и результаты эксперимента находят свое отражение в двумерном распределении частот.
Уравнение поверхности называется двумерным нормальным распределением (гладкая непрерывная колоколообразная поверхность)
Характеристики нормального распределения
Распределение значений x без учета значений y есть нормальное распределение;
Распределение значений y без учета значений x, тоже нормальное распределение;
Для каждого фиксированного значения x значение y дают нормальное распределение с дисперсией
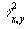
;
Для каждого фиксированного значения y значение x распределяется нормально с дисперсией
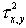
;
Среднее значения y для каждого отдельного значения x ложатся на переменную.
Меры изменчивости
При решении вопроса о наличии взаимосвязи (корреляции) между двумя переменными, руководствуются несколькими коэффициентами. Связь, выраженная графически, называется диаграммной рассеивания, где x – оценка IQ, y – оценка теста по математике.
Положение каждого объекта на диаграмме распределения определяется парой значений xi, yi и выражаются по отношению к мере центральной тенденции величинами 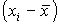 ,
, 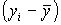 . Если объект имеет высокие показатели по обеим переменным, то эти величины получаются большими и положительными, в противном случае, если xi, yi малы, то разность большой и отрицательной.
. Если объект имеет высокие показатели по обеим переменным, то эти величины получаются большими и положительными, в противном случае, если xi, yi малы, то разность большой и отрицательной.
В дальнейшем будем говорить о произведении этих разностей и в том случае когда наблюдается прямая связь между этими переменными, произведение будет большим и положительным, следовательно такой же будет и сумма этих произведений 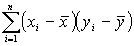 .
.
В случае обратной связи, когда большим значениям yi соответствуют малые значения xi и наоборот, в этом случае произведение разностей будет большим и отрицательным и сумма разностей также будет большой и отрицательной.
Если между переменными не наблюдается какой-либо связи , количество положительных и отрицательных произведений примерно рано и сумма их близка к нулю. Таким образом большая положительная сумма – жесткая прямая зависимость; большая отрицательная сумма – сильная обратная зависимость; близость к нулю – отсутствие зависимости.
Недостатком этой меры является то, что ее величина зависит от числа пар переменных x участвующих в расчетах.
Чтобы избежать связь независимого состояния V групп, мы усредняем эти значения:
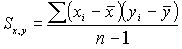
-
ковариация
Частный случай, ковариация переменной с самой сабой – дисперсия
Чтобы избавить меру связи от отклонений двух групп значений:
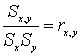
-
коэффициент
кореляции Пирсона или произведение моментов.
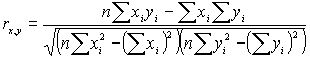
Значение коэффициента Пирсона не может выйти за границы интервала (-1; 1).
Влияние линейного преобразования переменных на коэффициент кореляции
Вместо xi вводим в формулу bx+ a, где a, b – коэффициенты, для yi вводим в формулу dy+ c, где c, d – коэффициенты.
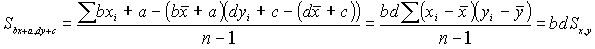
Рекомендуем скачать другие рефераты по теме: математика, ответ 2.
Предыдущая страница реферата |
2
3
4
5
6
7
8
9
10
11
12 |
Следующая страница реферата

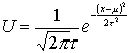
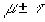
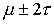
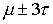
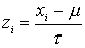 характеризуется распределением со средним равным нулю и стандартным отклонением равным 1. Площадь между двумя значениями x в нормальном распределении равна площади между ux стандартизованными величинами в единичном нормальном распределении. Нормализованную кривую изобрели для решения задач теории вероятности, но оказалось на практике, что она отлично аппроксимирует распределение черт при большом числе наблюдений для множества переменных. Можно предположить, сто не имея материальных ограничений на количество объектов и время проведения эксперимента, статистическое исследование приводило к нормально кривой.
характеризуется распределением со средним равным нулю и стандартным отклонением равным 1. Площадь между двумя значениями x в нормальном распределении равна площади между ux стандартизованными величинами в единичном нормальном распределении. Нормализованную кривую изобрели для решения задач теории вероятности, но оказалось на практике, что она отлично аппроксимирует распределение черт при большом числе наблюдений для множества переменных. Можно предположить, сто не имея материальных ограничений на количество объектов и время проведения эксперимента, статистическое исследование приводило к нормально кривой.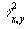 ;
Для каждого фиксированного значения y значение x распределяется нормально с дисперсией
;
Для каждого фиксированного значения y значение x распределяется нормально с дисперсией 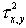 ;
Среднее значения y для каждого отдельного значения x ложатся на переменную.
Меры изменчивости
;
Среднее значения y для каждого отдельного значения x ложатся на переменную.
Меры изменчивости
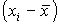 ,
, 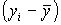 . Если объект имеет высокие показатели по обеим переменным, то эти величины получаются большими и положительными, в противном случае, если xi, yi малы, то разность большой и отрицательной.
. Если объект имеет высокие показатели по обеим переменным, то эти величины получаются большими и положительными, в противном случае, если xi, yi малы, то разность большой и отрицательной.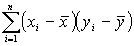 .
.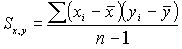 - ковариация
- ковариация
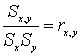 - коэффициент
кореляции Пирсона или произведение моментов.
- коэффициент
кореляции Пирсона или произведение моментов.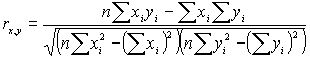
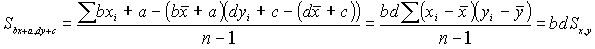
 Главная
Главная