Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



1. Сумма всех n-отклонений от значения среднего должно быть равно нулю, то есть:

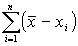
2. Если константу прибавить к каждому значению, то среднее увеличивается на ту же константу.

3. Если каждое значение умножить на константу, то среднее то же будет умножено на эту константу.

4. Сумма квадратов отклонений значений от их среднего меньше суммы квадратов отклонений от любой другой точки, то есть: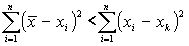

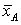Средняя медиана и мода для объединенных групп

- среднее для каждого класса, 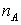- количество учащихся

Среднее общее группы:

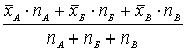
Для определения моды и медианы объединенной группы необходимы конкретные значения измерений.

Мода – это такое число в группе, с которым совпадает наибольшее количество значений в группе.

Медиана – это такая точка на числовой оси, для которой сумма абсолютных значений разности всех значений меньше суммы разностей для любой другой точки. Если именно так определять понятие ошибки, то медиана дает минимальную ошибку. Если же ошибка определяется как сумма квадратов разностей, то минимальную ошибку дает среднее.

Выбор меры центральной тенденции В малых группах мода очень нестабильна; На медиану не влияет величины очень больших и очень малых значений; На величину среднего влияет каждое значение; Некоторые множества данных не имеют меры центральной тенденции. Такая ситуация близка к бимодальной гистограмме или U-образной; Центральная тенденция групп, содержащая крайние значения наилучшим образом представляется в том случае, если гистограмма унимодальна; Если гистограмма симметрична и унимодальна, то средняя мода и медиана совпадают. Другие меры центральной тенденции

Среднее геометрическое: 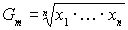;Среднегармоническое: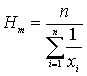

Меры изменчивости – второй момент характеризующий данные

Для оценки меры неоднородности (разброса, изменчивости), в группе вводят специальные меры, с помощью которых после их исследования можно уменьшить изменчивость данных. Первая из мер изменчивости называется размахом.

Размах – это разность максимального и минимального значений в группе.

Включающий размах – это разность между естественной верхней границей интервала, включая наибольшее значение, и естественной нижней границей, включая наименьшее значение интервала. 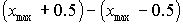. Включающий размах отличается от исключающего на единицу.

Размах от 90-го до 10-го процентеля: D = P90 – P10 . Эта мера более стабильна, чем предыдущая, так как на нее влияет множество значений.

Полу-междуквантильный размах: 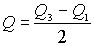, Q используется в распределениях, которые симметричны относительно медианы и среднего, для корректировки границ.

Дисперсия. Каждая из предыдущих мер возрастает с ростом рассеяния и уменьшается однородностей. Дисперсию, в отличие от предыдущих мер, используют при вычислении каждого из полученных измерений. Вычисляются значения отклонений 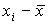и чтобы при суммировании 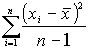не потерять величины этих отклонений, разница возводится в квадрат, поскольку мы оцениваем отклонение каждого измерения, делим на количество измерений. Обозначается дисперсия как .

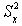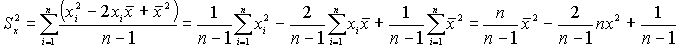
Для вычисления дисперсии не нужно вычислять среднее.

Дисперсия при сгруппированных данных вычисляется по такой же формуле, но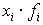

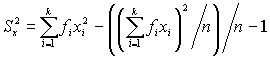
i изменяется от 1 до k, где k – количество разных значений .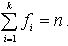

Стандартное отклонение: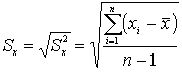

Для унимодальных симметричных распределений почти 70% значений лежит в интервале .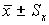

Свойства дисперсии:

1. Влияние на дисперсию увеличения каждого значения на какую либо константу:

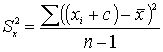, после выполнения математических операций убеждаемся, что дисперсия не изменяется.

2. Изменение дисперсии при умножении каждого исходного значения на константу:

Рекомендуем скачать другие рефераты по теме: математика, ответ 2.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата