Предыдущая страница реферата | 20  21  22  23  24  25  26  27  28  29  30 | Следующая страница реферата



 

 

2n отрезков.

Если в результате испытания случайная величена X попала в отрезок с начальной вершиной xi, то случайная величена X* приняла значение x (xi) с точностью до бесконечно малой D x - длины i-го отрезка. Вероятность того, что Y* примет значение x (xi) с точностью до бесконечно малой более высокого порядка, чем D x, тем более точно Y* аппроксимирует Y.

Вероятность наступления x (xi) для Y* равна

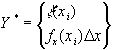
, при эта сумма переходит в .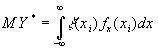

Тогда .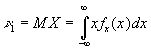

Самим показать, что все свойства мат. ожидания для дискретной случайной величены сохраняются для непрерывной случайной величены.

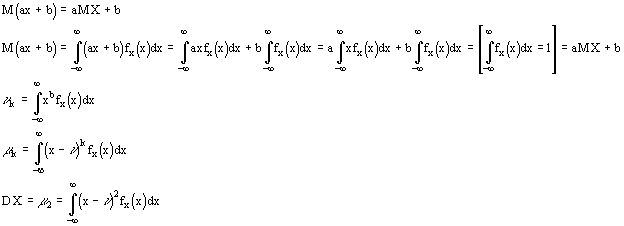
Доказать, что

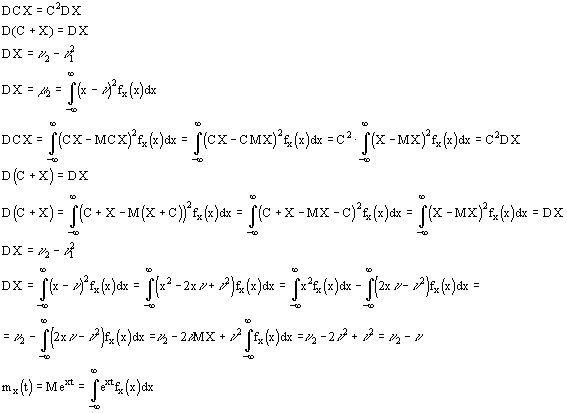
Доказать самим, что свойство 1 и 2 для производящей функции в дискретном случае справедливы и для непрерывного.

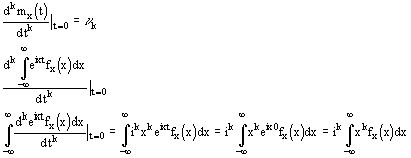
Распределение Гаусса - нормальное

Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности

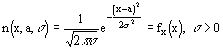
Из определения

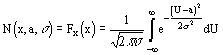
функция распределения

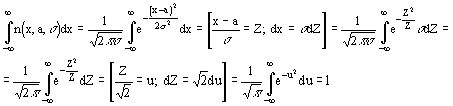
Найдем выражение для производящей функции нормального распределения

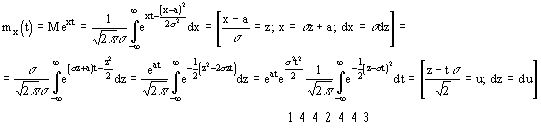
=1 (интеграл Эйлера)

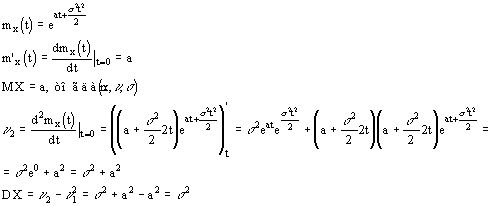
Изобразим примерный вид плотности

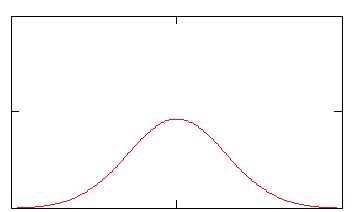
Рассмотрим центрированную нормальную величину, т.е. MX=0

У центральной нормированной величины все нечетные начальные моменты равны 0

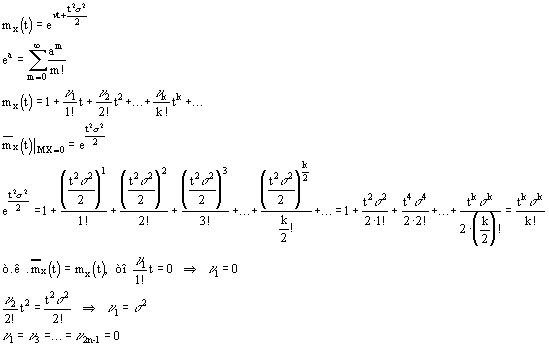
Функция Лапласа

Функцией Лапласа называется функция вида

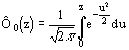
Свойства:

1) при z>0 функция Лапласа определяет вероятность попадания нормальной случайной величины с параметрами

MX=0

DX=1

в интервале (0, z)

2)

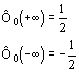
3) - функция нечетная

Иногда в литературе встречаются два вида функций Лапласа

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.

Предыдущая страница реферата | 20  21  22  23  24  25  26  27  28  29  30 | Следующая страница реферата