Теория вероятности и математическая статистика
| Категория реферата: Рефераты по математике
| Теги реферата: банк рефератов, шпаргалки по педагогике
| Добавил(а) на сайт: Долженко.
Предыдущая страница реферата | 23 24 25 26 27 28 29 30 31 32 33 | Следующая страница реферата
Следствием этого определения является следующее: любое сложное событие размерности 1 (произвольная кривая, принадлежащая пространству элементарных событий) имеет нулевую вероятность т.к. в противном случае вероятность достоверного события никогда бы не равнялась единице. Числовая скалярная функция двух действительных аргументов называется двумерной плотностью вероятности, двумерной случайной величины XY, если для фиксированных значений своих аргументов она выполняет равенство 
. Приведенное здесь определение является аналогичным определению одномерной плотности вероятности.
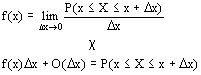
Ниже будет выведено условие существования плотности вероятности для фиксированных x, y.
Рассмотрим произвольную область G.
Разобьем область G на множество прямоугольников, покрывающих область G. Тогда на основании 3-й аксиомы теории вероятности имеем: вероятность искомого события равна:
. Точное выражение получим перейдя к пределу: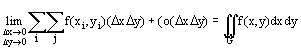 
(показать самим).
Числовая скалярная функция двух действительных аргументов называется двумерной функцией распределения, если она при фиксированном числе своих аргументов численно равна вероятности наступления Fx,y(x,y)=P(X£ x, Y£ y), если X, y - непрерывные случайные величины, то значение функции распределения не изменится.
Доказать:
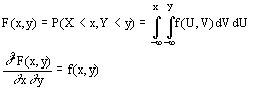
По определению второй смешанной производной.
Найдем по двумерной плотности одномерные плотности случайных величин X и Y.
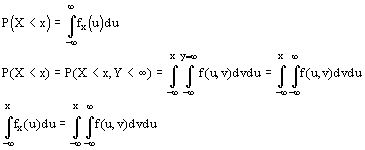
Т.к. полученное равенство верно для всех х, то подинтегральные выражение
аналогично
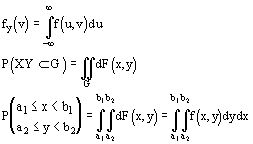
В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем курсе мы исследуем только 2 конструкции - дискретные или непрерывные, то для них полученные формулы эквивалентны и не имеет смысла какую-то из них вводить как первичную.
Условная плотность вероятности.
Найдем плотность вероятности случайной величины Y при условии, что в результате испытания над случайной величиной XY , X приняло значение х.
Обозначим
Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.
Категории:
Предыдущая страница реферата | 23 24 25 26 27 28 29 30 31 32 33 | Следующая страница реферата
Главная