Предыдущая страница реферата | 24  25  26  27  28  29  30  31  32  33  34 | Следующая страница реферата

Математическое ожидание скалярной функции случайных аргументов.

Двумерный дискретный случай.

XY

Числовая скалярная функция

является одномерной дискретной случайной величиной, со следующим отличием от обычного представления:

для того, чтобы в испытании получить реализацию необходимо провести испытание над двумерной случайной величиной XY, зафиксировать ее результат xi,yi и подставить в . Полученное число и есть реализация случайной величины .

Таблица случайной величины строится по таблице

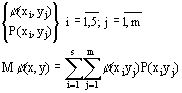
Двумерные непрерывные случайные величины

Случайную величину аппроксимируем дискретной по следующему правилу:

пространство элементарных событий XY представим в виде совокупности прямоугольников с вершинами , если в результате испытания XY попало в прямоугольник (i,j), то эта случайная величина приняла значение . Вероятность наступления этого события равна:

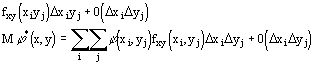
точное значение мат. ожидания

 

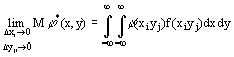
n-мерный дискретный случай

- многомерная дискретная случайная величина

Найдем

Вероятностное пространство зададим в виде

Тогда

 

n-мерный непрерывный случай

Теорема 1. Математическое ожидание суммы случайных величин равно сумме математических ожиданий

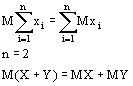
а) дискретный случай

б) непрерывный случай

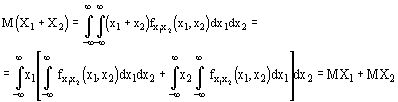
Пусть n-произвольное число

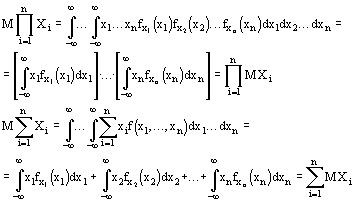
Теорема 2. Математическое ожидание произведения независимых случайных величин равно произведению мат.ожиданий.

По определению имеем т.к. случайные величины X и Y независимы, то

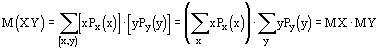
Коэффициент ковариации

Коэффициентом ковариации называется выражение

Эта формула верна, т.к. верна следующая формула.

Пусть

тогда

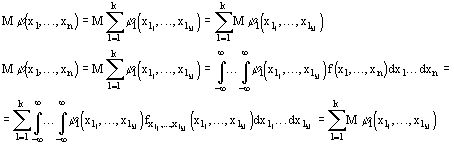
Если случайные величины XY независимы, то их коэффициент ковариации равен нулю, обратное в общем случае неверно.

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.

Предыдущая страница реферата | 24  25  26  27  28  29  30  31  32  33  34 | Следующая страница реферата