Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата

Уравнения, которые решаются

Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.

            В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:

Если несократимая дробь  является корнем многочлена  с целыми коэффициентами, то ее числитель  является делителем свободного члена , а знаменатель  - делителем старшего коэффициента .

           

Для доказательства достаточно подставить в уравнение   и умножить уравнение на . Получим

.

Все слагаемые в левой части, кроме последнего, делятся на , поэтому и  делится на , а поскольку  и  - взаимно простые числа,  является делителем . Доказательство для  аналогично.

            С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа "кандидатов". Например, для уравнения

,

старший коэффициент которого равен 1, "кандидатами" будут делители числа –2. Их всего четыре: 1, -1, 2 и –2. Проверка показывает, что корнем является только одно из этих чисел: .

Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,

остаток от деления многочлена  на двучлен  равен , т. е. .

Из теоремы непосредственно следует, что

Если  - корень многочлена , то многочлен делится на , т. е. , где  - многочлен степени, на 1 меньшей, чем .

           

Продолжая наш пример, вынесем из многочлена

множитель . Чтобы найти частное , можно выполнить деление "уголком":

                                                          

                                                                      

          

                                                                    

                                                                    

                                                                         

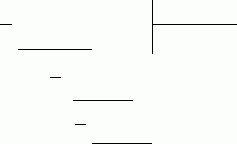
Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, ответы 7 класс.





Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата