Уравнения и способы их решения

| Категория реферата: Рефераты по математике
| Теги реферата: новшество, шпаргалки бесплатно
| Добавил(а) на сайт: Рубашкин.

Предыдущая страница реферата | 9 10 11 12 13 14 15 16 17 18 19 | Следующая страница реферата

Но есть и более простой способ. Он станет понятен из примера:

Теперь остается решить квадратное уравнение . Его корни:

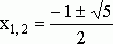Метод неопределенных коэффициентов

Если у многочлена с целыми коэффициентами рациональных корней не оказалось, можно попробовать разложить его на множители меньшей степени с целыми коэффициентами. Рассмотрим, например, уравнение

Представим левую часть в виде произведения двух квадратных трехчленов с неизвестными (неопределенными) коэффициентами:

Раскроем скобки в правой части и приведем подобные:

Теперь, приравнивая коэффициенты при одинаковых степенях в обеих частях, получим систему уравнений

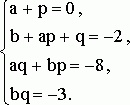
Попытка решить эту систему в общем виде вернула бы нас назад, к решению исходного уравнения. Но целые корни, если они существуют, нетрудно найти и подбором. Не ограничивая общности, можно считать, что , тогда последнее уравнение показывает, что надо рассмотреть лишь два варианта: , и . Подставляя эти пары значений в остальные уравнения, убеждаемся, что первая из них дает искомое разложение: . Этот способ решения называется методом неопределенных коэффициентов.

Если уравнение имеет вид , где и - многочлены, то замена сводит его решение к решению двух уравнений меньших степеней: и .

Возвратные уравнения

Возвратным алгебраическим уравнением называется уравнение четной степени вида

в которых коэффициенты, одинаково отстоят от концов, равны: , и т. д. Такое уравнение сводится к уравнению вдвое меньшей степени делением на и последующей заменой .