Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Формула Кардано

Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:

.

Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу :

, или

.

Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений

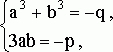 или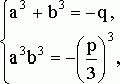

и взять в качестве  сумму  и . Заменой ,  эта система приводится к совсем простому виду:

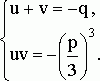
Дальше можно действовать по-разному, но все "дороги" приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного  квадратного уравнения равна коэффициенту при  со знаком минус, а произведение – свободному члену. Отсюда следует, что  и  - корни уравнения

.

Выпишем эти корни:

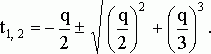
Переменные  и  равны кубическим корням из  и , а искомое решение кубического уравнения (13) – сумма этих корней:

.

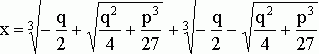Эта формула известная как формула Кардано.

Тригонометрическое решение

подстановкой  приводится к "неполному" виду

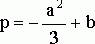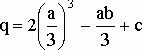                         ,   ,   .                         (14)

Корни , , "неполного" кубичного уравнения (14) равны

, ,

где

,    ,

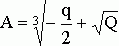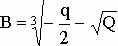Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, ответы 7 класс.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата