Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

            5) ().

Уравнение имеет один дествительный корень  и два комплексных корня

.

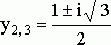            6)             ().

Уравнение действительных корней не имеет. Комплексные корни:

,  .

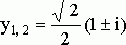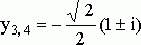Кубические уравнения

Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида

, где ,

оказались "крепким орешком". В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике "Сумма знаний по арифметике, геометрии, отношениям и пропорциональности" задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.

Начнем с упрощения

Если кубическое уравнение общего вида

, где ,

разделить на , то коэффициент при  станет равен 1. Поэтому в дальнейшем будем исходить из уравнения

                                                     .                                                     (11)

Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:

Чтобы не путаться в коэффициентах, заменим здесь  на  и перегруппируем слагаемые:

                                           .                                           (12)

Мы видим, что надлежащим выбором , а именно взяв , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при  и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:

.

Если здесь сделать замену , получим кубическое уравнение относительно  без члена с :

.

Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида

                                                            .                                                            (13)

Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, ответы 7 класс.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата