В
дискретной форме это уравнение (с точностью до членов второго порядка) будет
иметь вид [7]:
|
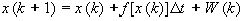 , ,
|
(19)
|
где
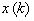
вектор состояния размерности
вектор состояния размерности 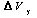 ,
,
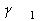
непрерывная векторная функция, которая по крайней мере дважды дифференцируема
по своим аргументам,
непрерывная векторная функция, которая по крайней мере дважды дифференцируема
по своим аргументам,
|
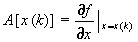 , ,
|
(20)
|
матрица
Якоби вектор-функции 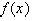 , a
, a 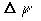 отражает
погрешность дискретизации и неопределенности моделирования в уравнении
динамики. Предполагается, что
отражает
погрешность дискретизации и неопределенности моделирования в уравнении
динамики. Предполагается, что 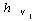 является белой
гауссовской последовательностью с нулевым средним и матрицей ковариации
является белой
гауссовской последовательностью с нулевым средним и матрицей ковариации 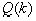 :
:
|
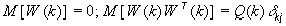 , ,
|
(21)
|
|
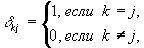
|
|
где
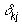
дельта-функция Кронекера.
дельта-функция Кронекера.
Начальное
значение вектора состояния 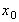 принимается
гауссовской
слу
чай
ной
переменной с известными средним значением и матрицей ковариации вида:
принимается
гауссовской
слу
чай
ной
переменной с известными средним значением и матрицей ковариации вида:
|
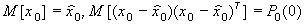
|
(22)
|
Процесс
измерения описывается уравнением:
|
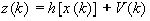 , ,
|
(23)
|
|
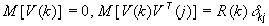 , ,
|
|
где
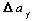
вектор погрешностей измерений типа белой последовательности с нулевым средним и
матрицей ковариации
вектор погрешностей измерений типа белой последовательности с нулевым средним и
матрицей ковариации 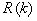 ,
, 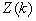
вектор размерности
вектор размерности 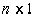 ,
, 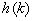
непрерывная векторная функция, дважды дифференцируемая по своим аргументам.
непрерывная векторная функция, дважды дифференцируемая по своим аргументам.
Тогда
обобщенный калмановский фильтр описывается следующими
уравнен
иями:

 Главная
Главная