где
индекс 1 относится к ведущему ЛА, а индекс 2
к ведомому.
3. Синтез алгоритмов обработки информации
Рассмотрим
следующий вариант построения алгоритмов управления. Он связан с разработкой
алгоритмов оценивания параметров движения ведущего ЛА
по
результатам измерений относительного движения. Поскольку измерения содержат
случайные ошибки, а алгоритм оценки должен быть эффективным в смысле их
снижения и снижения влияния этих ошибок на точность получаемых оценок
параметров движения ведущего ЛА, то есть алгоритм обработки
информации должен обеспечивать фильтрацию ошибок измерений и идентификацию
параметров движения ведущего ЛА.
В
общем случае алгоритм оценки и идентификации включает в себя блоки первичной и
вторичной обработки измерительной информации. Ввиду того, что блок первичной
обработки является составной частью измерительной системы и конструктивно с ней
совмещен, то алгоритм первичной обработки информации здесь не рассматривается.
Основное внимание при дальнейших исследованиях уделяется методам вторичной
обработки информации по результатам первичных измерений.
Сначала
рассмотрим общие вопросы идентификации моделей динамических систем. Задачу
идентификации [5] или, другими словами, задачу оценивания параметров
динамической системы можно сформулировать как задачу оценивания параметров
модели системы, которая обладает существенными чертами проектируемой системы и
представляет знания об этой системе в удобной форме. То есть целью
идентификации не является абсолютно точное математическое описание физической
реальности, а лишь создание модели, отражающей существенные для дальнейшего
применения свойства системы. Положение существенно усложняется, если
дополнительно с вектором параметров необходимо оценивать и вектор состояния.
Здесь следует обратить внимание
на то, что идентификация
параметров даже для линейных систем приводит
к нелинейным
методам оценивания и идентификации.
В
настоящее время опубликовано значительное число работ математического характера
по оптимальной нелинейной фильтрации.
Наиболее общее решение
проблемы нелинейной фильтрации получено Р.Л.Стратоновичем
в
его работах по теории условных марковских процессов [6]. Как показано в работе
[6], получение оптимальной нелинейной оценки сводится к решению функционального
рекуррентного соотношения для апостериорной плотности вероятности. Основной
особенностью задач нелинейной фильтрации является то, что реализация
оптимальных алгоритмов обработки информации на современном уровне развития
вычислительной техники не представляется возможной из-за сложности решения
уравнений для апостериорной плотности вероятности, включающим многомерное
интегрирование. Этот факт обусловил появление большого числа работ, посвященных
разработке субоптимальных алгоритмов нелинейной фильтрации, основанных на
различных аппроксимациях апостериорной плотности вероятности. Разработка
субоптимальных алгоритмов диктуется также необходимостью реализации их в
системах, работающих в реальном времени и удобством реализации на ЦВМ. С этой
точки зрения предпочтительны рекуррентные методы, требующие запоминания на
каждом такте сравнительно небольшого числа результатов вычислений.
Рассмотрим
теперь конкретно задачу построения алгоритмов CMCН ДПЛА с
идентификатором в контуре управления. Имеется несколько вариантов синтеза. В
этом случае задача сводится к отысканию расчетных соотношений для параметров 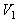 ,
, 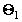 ,
, 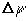 ,
, 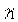 ,
, 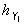 ,
, 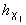 ,
, 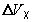 ,
, 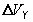 ,
, 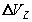 ,
, 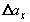 ,
, 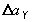 ,
, 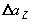 в
предположении, что имеется информация о параметрах относительного движения
в
предположении, что имеется информация о параметрах относительного движения 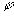 ,
, 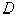 ,
, 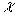 ,
, 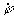 ,
, 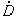 ,
, 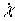 , измеренных с
помехами, и параметрах полета ведомого ЛА. Указанные параметры необходимы для
реализации алгоритмов СМСН.
, измеренных с
помехами, и параметрах полета ведомого ЛА. Указанные параметры необходимы для
реализации алгоритмов СМСН.
Рассмотрим
относительное движение двух ЛА в пространстве. В этом случае изменение углов
места и азимута, дальности, угловых скоростей линии визирования, радиальной
скорости описывается в основной СК системой уравнений вида:
где
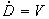 ,
, 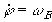 ,
, 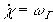 .
.
Эта
система может быть положена в основу синтеза алгоритмов нелинейной фильтрации
для получения оценок 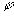 ,
, 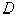 ,
, 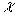 , идентификации
, идентификации 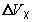 ,
, 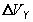 ,
, 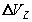 ,
, 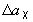 ,
, 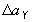 ,
, 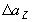 .
.
Для
вычисления оценок парамет
ров 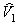 ,
, 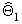 ,
, 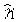 ,
, 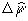 ,
, 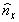 ,
, 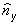 , и т.д.
необходимо определить математические ожидания этих функций на основе плотности
распределения оценок
, и т.д.
необходимо определить математические ожидания этих функций на основе плотности
распределения оценок 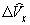 ,
, 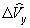 ,
, 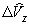 ,
, 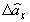 ,
, 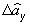 ,
, 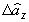 . Поскольку
этот путь связан с громоздкими вычислениями многомерных интегралов, можно
использовать более простой, но приближенный способ, согласно которому оценки
перечисленных параметров вычисляются по определенным формулам, куда в качестве
. Поскольку
этот путь связан с громоздкими вычислениями многомерных интегралов, можно
использовать более простой, но приближенный способ, согласно которому оценки
перечисленных параметров вычисляются по определенным формулам, куда в качестве 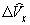 ,
, 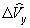 ,
, 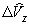 ,
, 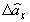 ,
, 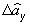 ,
, 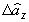 входят их
оценки. Используя информацию об этих оценках, можно определить значения
относительных скоростей и ускорений в траекторной СК ведущего ЛА, сформировать
программные значения.
входят их
оценки. Используя информацию об этих оценках, можно определить значения
относительных скоростей и ускорений в траекторной СК ведущего ЛА, сформировать
программные значения.
Таким
образом, основная задача состоит в определении оценок 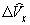 ,
, 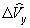 ,
, 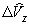 ,
, 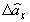 ,
, 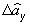 ,
, 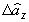 . Конкретному
рассмотрению алгоритмов оценивания и идентификации параметров относительного
движения ЛА предпошлем краткое изложение некоторых общих принципов их
построения.
. Конкретному
рассмотрению алгоритмов оценивания и идентификации параметров относительного
движения ЛА предпошлем краткое изложение некоторых общих принципов их
построения.
Методически
исследование по выбору алгоритмов обработки ин
формации в СМСН
ДПЛА проводилось по следующей схеме Это, в первую очередь, касалось замены
исходной нелинейной модели состояния и наблюдений тем или иным приближением и
построение алгоритма оценивания на основе такой аппроксимации. Во-первых, для
решения поставленной проблемы используется подход, основанный на дискретной
аппроксимации динамической модели относительного движения. Это позволяет
наиболее эффективно реализовать алгоритмы нелинейной фильтрации в БЦВМ, в
основу которых положены дискретные методы оценивания. Во-вторых, нелинейные
уравнения модели и наблюдений раскладываются в ряд Тейлора до членов первого
порядка включительно относительно оценки на предыдущем шаге. В-третьих, в
качестве математических моделей идентифицируемых параметров системы
используются локальные модели, описывающие изменения параметров лишь в узком
диапазоне изменения времени. Простейшей локальной моделью изменения параметров
является следующая:

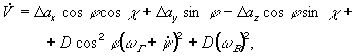
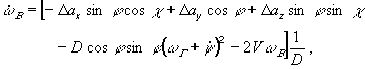
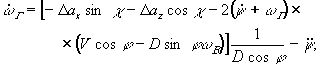
 Главная
Главная