В данной постановке задача квадратичного программирования всегда имеет оптимальный вектор, и является задачей выпуклого программирования с линейными ограничениями типа равенств.
3.2 Условия оптимальности в задаче (3.2)
Условия оптимальности в задаче (3.2) представляют собой формулировку условий Куна-Таккера для этой задачи. Будем рассматривать следующую форму записи условий Куна-Таккера для задачи выпуклого программирования:
|
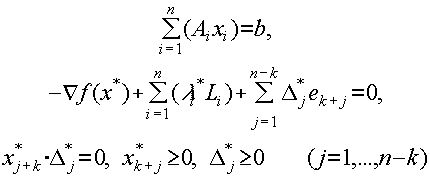
|
(3.2.1) |
В нашем случае получим:
|
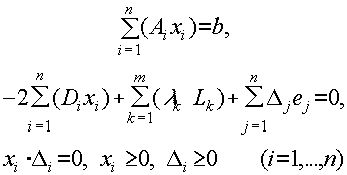
|
(3.2.2) |
Здесь Ai- столбцы матрицы A длины m, Di столбцы матрицы D длины n, Lk - строки матрицы A длины n, ej - n-мерные столбцы единичной матрицы. Здесь и далее xi - компоненты оптимального вектора задачи x, l
k и D
k - множители Лагранжа условий Куна-Таккера. Запишем систему 3.2.2 в более обобщенной форме:
|
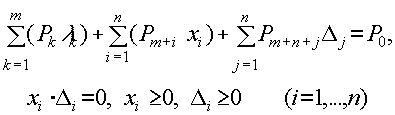
|
(3.2.3)
|
где составные столбцы P0, ... Pm+2n каждый длиной m+n являются столбцами блочной матрицы P, имеющей следующий вид:
|
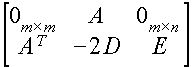
|
(3.2.4) |
Рекомендуем скачать другие рефераты по теме: реферат предприятие, реферат по русскому.
Предыдущая страница реферата |
1
2
3
4
5
6
7
8
9
10
11 |
Следующая страница реферата

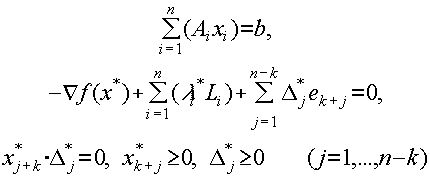
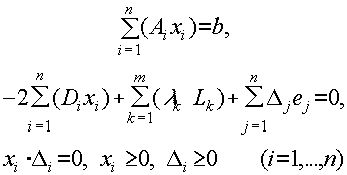
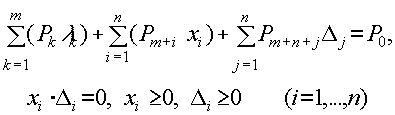
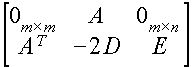
 Главная
Главная