
Формирование инвестиционного портфеля
| Категория реферата: Рефераты по информатике, программированию
| Теги реферата: bestreferat ru, реферат катастрофы
| Добавил(а) на сайт: Альбертина.
Предыдущая страница реферата | 5 6 7 8 9 10 11 12 13 14 15 | Следующая страница реферата
|
|
(3.5.3) |
Если множество UÁ порождает базис, вследствие (3.5.3) поиск минимума на многообразии XÁ представляет собой разложение вектора P0 по этому базису, т.е. эквивалентен решению системы линейных уравнений. Таким образом, метод субоптимизации на многообразиях в случае задачи квадратичного программирования оказывается эффективным в том случае, если в цепочке итерационного процесса встречаются только множества индексов, порождающие базисы.
Процедура метода строится на двух основных операциях, аналогичных блокам общего алгоритма субоптимизации на многообразиях для задачи выпуклого программирования.
Операция А. Пусть для некоторого набора индексов Á 0 определена оптимальная точка x* и множители Лагранжа l *k и D *j удовлетворяющие условиям Куна-Таккера совместно с оптимальным вектором x. Рассмотрим вспомогательное многообразие
|
|
(3.5.4) |
Операция А состоит в нахождении оптимального вектора x*(q ), а также множителей Лагранжа, удовлетворяющих условиям Куна-Таккера задачи минимизации квадратичного функционала на многообразии (3.5.4).
Запишем условия Куна-Таккера для этой вспомогательной задачи:
|
|
Если набор индексов Á 0 порождает базис, то существует разложение вектора Pm+j0 по этому базису, имеющее следующий вид:
|
|
(3.5.6) |
Подставляя это разложение в (3.5.5), и учитывая оптимальность набора x*,l *,D *, получаем следующие выражения для компонент оптимальной точки на многообразии (3.5.4):
|
|
Категории:Предыдущая страница реферата | 5 6 7 8 9 10 11 12 13 14 15 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
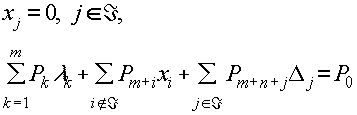
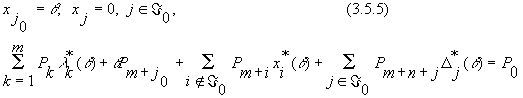
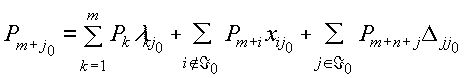
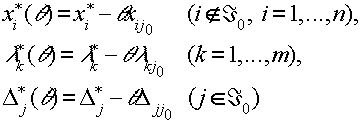
 Главная
Главная