Формирование инвестиционного портфеля
| Категория реферата: Рефераты по информатике, программированию
| Теги реферата: bestreferat ru, реферат катастрофы
| Добавил(а) на сайт: Альбертина.
Предыдущая страница реферата | 7 8 9 10 11 12 13 14 15 16 17 | Следующая страница реферата
то условиям Куна-Таккера для задачи (3.5.1) соответствующей набору индексов Á 1 , удовлетворяют переменные, получаемые с помощью следующих формул:
|
|
(3.5.13) |
где
|
|
(3.5.14) |
Учитывая вышеописанные условия, операция Б оказывается осуществимой в том случае, когда наборам индексов Á 0 и Á 1 соответствует базис UÁ 1,Á 0 . Операция Б является аналогом блока 4 общей схемы метода субоптимизации на многообразиях для задачи выпуклого программирования.
Для большей наглядности можно определить множество LÁ 1,Á 0 представляющее собой прямую, порождаемую базисом UÁ 1,Á 0 следующего вида:
|
|
(3.5.15) |
Здесь 
- коэффициенты разложения вектора P0, а xir - вектора Pm+n+r по базису UÁ
1,Á
0. Заметим, что LÁ
1,Á
0(0) есть оптимальный вектор многообразия (3.5.4) при q
= 
. Переход от этой точки к новому многообразию с помощью операции Б представляет собой движение по указанной прямой от дельта равного нулю в положительную (как будет показано позже) сторону.
3.6. Метод субоптимизации на многообразиях в задаче квадратичного программирования. Теоретическое обоснование.
Заметим, что если множество индексов Á порождает базис UÁ , то задача (3.5.1), соответствующая этому множеству индексов имеет единственный оптимальный вектор x* , обладая при этом свойством единственности, введенным ранее для задачи выпуклого программирования.
Выше были описаны вспомогательные задачи метода субоптимизации на многообразиях, однако не были сформулированы правила применения этих операций. Ниже будут доказаны две теоремы, дающие способ определения неизвестных шагов q и d . Для их доказательства потребуется несколько вспомогательных утверждений.
Лемма 1. Пусть вектора x0, x1 удовлетворяют системе уравнений условий Куна-Таккера и пусть f(x) - неотрицательно определенный квадратичный функционал вида xTDx, а D 1 вектор ограниценных по знаку множителей Лагранжа, удовлетворяющих условиям Куна-Таккера совместно с вектором x1 . Тогда имеет место следующее неравенство:
|
|
Категории:Предыдущая страница реферата | 7 8 9 10 11 12 13 14 15 16 17 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
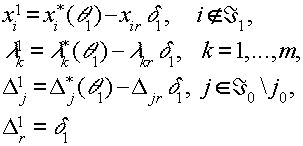
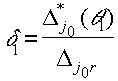
Главная