Таким образом, в случае, если набор индексов Á
0 порождает базис, операция А осуществляется тривиально, и определяется выражениями (3.5.7).
Суть операции А состоит в нахождении оптимальной точки на новом многообразии (3.5.4) по известной оптимальной точке на многообразии (3.4.4).
Операция Б. Пусть некоторое вспомогательное многообразие XÁ
0(q
1) таково, что одна из базисных компонент вектора x обратилась в ноль:
|
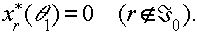
|
(3.5.8) |
Суть операции Б состоит в переходе от многообразия XÁ
0(q
1) к другому многообразию XÁ
1 , соответствующему набору индексов Á
1 , определяемому следующим образом:
|
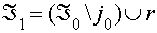
|
(3.5.9) |
т.е. индекс j0 из (3.5.4) заменяется на индекс r из (3.5.8).
Учитывая (3.5.8), разложение (3.5.5) на многообразии XÁ
0 можно представить следующим образом:
|
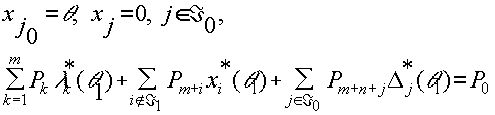
|
(3.5.10) |
Аналогично случаю, рассмотренному в операции А, что, если имеет место разложение:
|
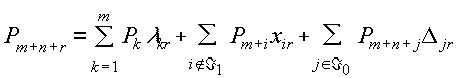
|
(3.5.11) |
причем выполнено соотношение
|
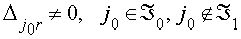
|
(3.5.12) |
Рекомендуем скачать другие рефераты по теме: реферат предприятие, реферат по русскому.
Предыдущая страница реферата |
6
7
8
9
10
11
12
13
14
15
16 |
Следующая страница реферата

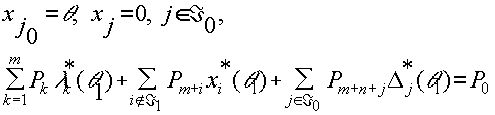
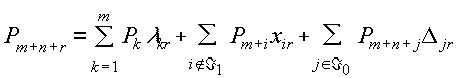
 Главная
Главная