Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.

На практике редко удается вычислить точно определенный интеграл. Например, в элементарных функциях не вычисляется функция Лапласа

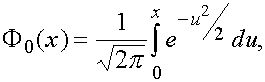
широко используемая в теории вероятностей для вычисления вероятностей, связанных с нормально распределенными случайными величинами.

Рассмотрим некотрые широко используемые приемы приближенного вычисления определенных интегралов.

Квадратурные формулы.

Введем понятие квадратурные формулы. Пусть дан определенный интеграл

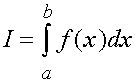(1)

от непрерывной на отрезке функции . Приближенное неравенство

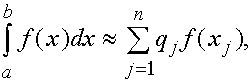(2)

где - некоторые числа, - некотрые точки отрезка , называется квадратурной формулой, определяемой весами и узлами .

Говорят, что квадратурная формула точна для многочленов степени , если при замене на произвольный алгебраический многочлен степени приближенное равенство (2) становится точным.

Рассмотрим наиболее простые квадратурные формулы.

Формула прямоугольников. Допустим, что . Положим приближенно

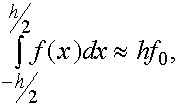(3)

где , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции , аппроксимируется площадью прямоугольника, высота которого равна значению в средней точке основания трапеции .

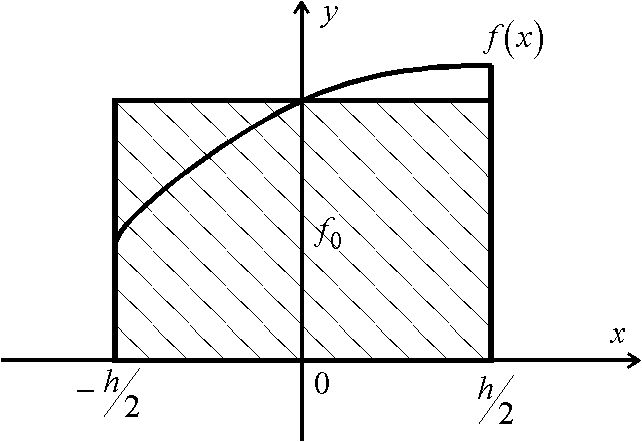
Найдем остаточный член , т.е. погрешность формулы (3) .

Пусть

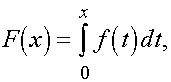(4)

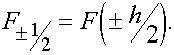Так как

то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем

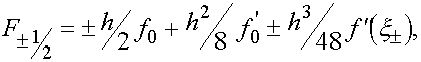(5)

Рекомендуем скачать другие рефераты по теме: ответы школа, свобода реферат.





Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата