Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  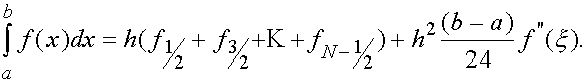22

(22) Совершенно àíàëîãè÷íî при услвии, что с использованием формул (7), (14) получается усложненная квадратурная формула трапеций

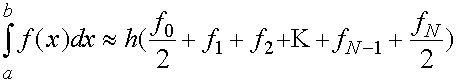(23)

и отвечающая ей формула с остаточным членом

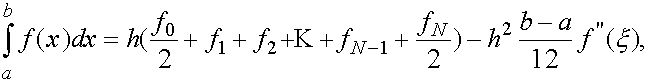(24)

где некоторая точка.

Пусть теперь 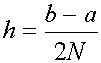и, как обычно, Перепишем каноническую квадратурную формулу Симпсона (15) применительно к отрезку длины :

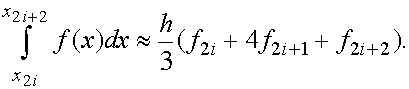
Суммируя левую и правую части этого соотношения от 0 до

N-1, получаем усложненную квадратурную формулу Симпсона (25)

Сответствующая ей формула с остаточным членом, полученная суммированием по частичным отрезкам равенств вида (18), при условии, что , такова :

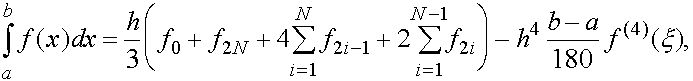(26)

где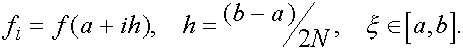

Введем краткие обозначения

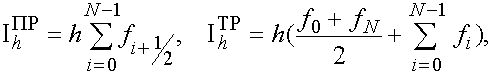(27)

где а также положим

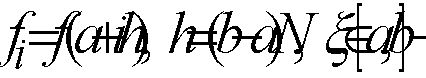(28)

где

Приближенные равенства

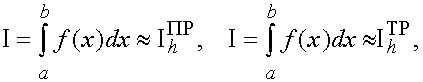(29)

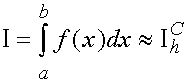(30)

назовем сответственно формулами прямоугольников, трапеций и формулой Симпсона, опуская слова ‘’усложненная квадратурная’’.

Из виражений остаточных членов в (22), (24), (26) видно, что формулы (29) прямоугольников трапеций точны для многочленов первой степени, т.е. для линейных функций, а формула (30) Симпсона точна для многочленов третьей степени (для них остаточный член равен нулю ). Погрешность формул (29) имеет второй порядок относительно (заведомо не лучше, если непрерывна на и не обращается в нуль), а формула Симпсона при соответствующей гладкости является формулой четвертого порядка точности. Поэтму для функций класса при малом формула Симпсона обычно дает более высокую точность, чем формула (29).

Погрешность формулы прямугольников и формулы Симпсона при вычислении интеграла (1) в силу (22), (26) удовлетворяет неравенствам

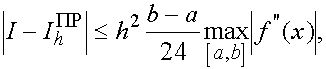(31)

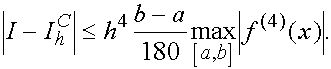(32)

Аналогичное неравенство имеет место и для погрешности формули трапеций.

Наряду с оценками погрешноси сверху полезны оценки снизу. В частности, для погрешности формулы прямоугольников оценка снизу, вытекающая из (22), такова:

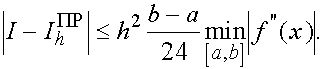(33)

Пример. Исследовать погрешность квадратурных формул для интеграла

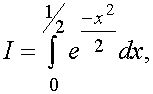при .

 

Имеем

о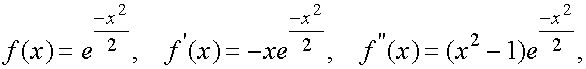

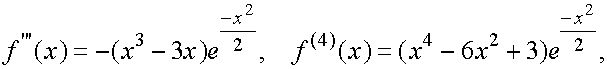
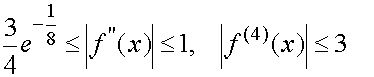на

Согласно (31)-(33) получаем

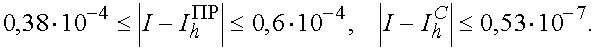
Формулы прямоугольников трапеций в отдельности уступают при интегрировании гладких функций формуле Симпсона. Однако в паре они обладают ценным качеством, а именно, если не изменяет знака на то формулы (29) дают двусторонние приближения для интеграла (1), так как согласно (22), (24) их остаточные члены имеют противоположные знаки.

В рассмотренном примере Поэтому

В данной ситуации естественно положить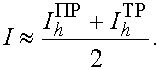

Тогда 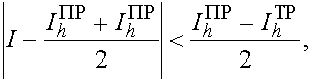т.е. погрешность оценивается через самые приближенные значения интеграла.

 

 

 

Скачали данный реферат: Zarema, Martiniana, Дормидбнт, Бысов, Jakutkin, Karjukin.
Последние просмотренные рефераты на тему: чс реферат, доклад, бесплатно реферат на тему, население реферат.





Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22