Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата

у которой по сравнению с матрицей переставлены l -я и (k-1 )-я строка l-й и ( k-1)- й стодбец. В результате на необходимом нам месте оказывается ненулевой элемент , уже преобразованная часть матрицы не меняется, можно применять обычный шаг метода Данилевского к матрице . Она подбна матрице (и, следовательно, исходной матрице А ), т.к. елементарная матрица перестановок совпадает со своей обратной, т.е.

Рассмотрим второй нерегулярный случай, когда в матрице ýлемент и все элементы этой строки, которые тоже находятся левее его, тоже равны нулю. В этом случае характеристический определитель матрицы можно представить в виде

где і - единичные матрицы соответствующей размерности, а квадратные матрицы и имееют вид:

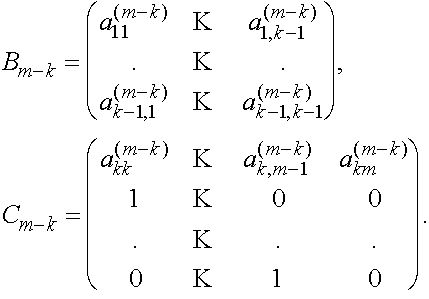
Обративм внимание на то, что матрица уже нормальную форму Фробениуса, и поэтому сомножитель просто развертывается в виде многочлена с коэффциентами, равными элементам первой строки.

Сомножитель , åñòü характеристический определитель матрицы . Для развертывания можн опять применять метод Данилевского, приводя матрицу подобными преобразованиями к нормальной форме Фробениуса.

Предположим теперь, что матрица А подобным преобразованиям

уже приведена к нормальной форме Фробениуса. Решая характеристическое уравнение

,

находим одним из известных методов его корни которые являются собственными значениями матрицы Р и исходной матрицы А.

Теперь стоит задача отыскать собственные векторы, соответствующие этим собственным значениям, т.е. векторы такие, что

Решим ее следующим образом: найдем собственные векторы матрицы Р , а затем по определенному соотношению я пересчитаем собственные векторы матрицы А . Это соотношение дает следующая теорема.

ТЕОРЕМА. Пусть є есть собственное значение , а есть соответствующий собственный вектор матрицы Р , которая подобна матрице А ,т.е.

Тогда есть собственный вектор матрицы А , соответствующий собственному значению

Доказательство.Тривиально следует из того, что

Домножая левую и правую часть этого равенства слева на S ,

имеем

А это и означает, что -собственный вектор матрицы А ,

отвечающий собственному значению

Íàéäåì ñîáñòâåííûé вектор матрицы Р , которая имеет нормальную форму Фробениуса и подобна матрице А. Записывая в развернутой форме, имеем

Рекомендуем скачать другие рефераты по теме: ответы школа, свобода реферат.





Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата