Численные методы

| Категория реферата: Рефераты по математике
| Теги реферата: контрольные работы 9 класс, шпаргалки по экономике
| Добавил(а) на сайт: Карев.

Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата

где -неизвестные коэффициенты, которые последовательно находятся от до (прямая прогонка ), а затем последовательно вычисляются (обратная прогонка) .

Выведем формулы для вычисления Из (3) можно получить

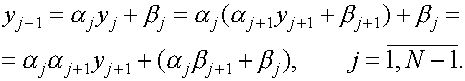
Подставляя имеющиеся выражения для в уравнение (1),приходим при к уравнению Последнее уравнение будет выполнено если коэффициенты выбрать такими, чтобы выражения в квадратных скобках обращались в нуль.

А именно, достаточно положить 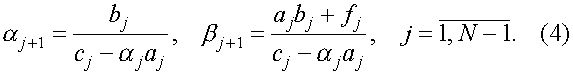Для отыскания всех достаточно задать

Эти начальные значения находим из требования эквивалентности условия (3) при т.е. условия , первому из уравнений (2).

Таким образом, получаем

(5)

Нахождение коэффициентов по формулам (4), (5) называется прямой прогонкой. После того, как прогоночные коэффициенты найдены, решение системи (1), (2) находится по рекуррентной формуле (3), начиная с Для начала счета по этой формуле требуется знать , которое определяется из уравнений

И равно

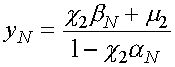Нахождение по формулам

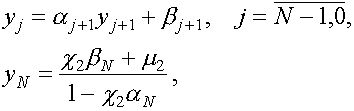(6)

называется обратной прогонкой. Алгоритм решения системы (1), (2) определяемый формулами (4)-(6) называется методом прогонки.

Метод прогонки можно пременять, если знаменатели выражений (4), (6) не обрщаются в нуль.

Покажем, что для возможности применения метод прогонки достаточно потребовать, чтобы коэффициенты системы (1), (2) удовлетворяли условиям

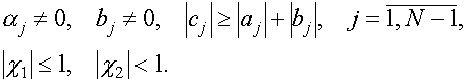(8)

Сначала докажем по индукции, что при условиях (7), (8) модули прогоночных коэффициентов не превосходят единицы. Согласно (5), (8) имеем . Предположим,что для некоторого и докажем, что