Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Например, для матрицы второго порядка система (2) распадается на две независимые системы:

Äëÿ ðåøåíèÿ систем (3) используется метод Гаусса ( обычный или с выбором главного элемента).

Рассмотрим применение метода Гаусса без выбора главного элемента. Поскольку все системы (3) имеют одну и ту же матрицу А , достаточно один раз совершить прямой ход метода Гаусса, т.е. получить разложение A=LU и запомнить матрицы L i U .

Обратный ход осуществляется путем решения систем уравнений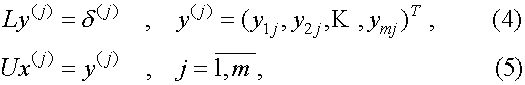

с треугольными матрицами L è U.

При осуществлении обратного хода можно сократить число действий, принимая во внимание специальный вид правых частей системы (4).

Запишем подробнее первые j-1 уравнений системы (4):

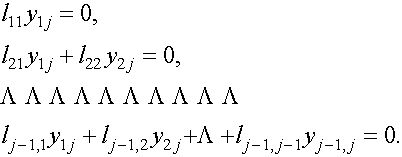
Учитывая невырожденность матрицы L ( т.е.

отсюда получаем

При этом оставшиеся уравнения системы (4) имеют вид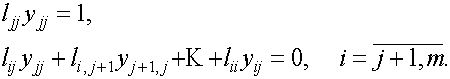

Отсюда последовательно находятся неизвестные по формулам: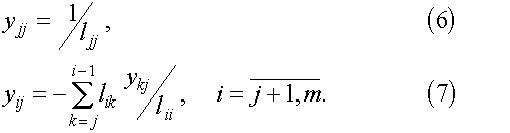

Можно показать, что общее число действий умножения и деления, необходимое для обращения матрицы указанным способом, порядка . Тем самым обращение матрицы требует не намного больше времени, чем решение системы уравнений.

МЕТОД ПРОГОНКИ.

Система уравнений для определения коэффициентов сплайна представляет собой частный случай систем линейных алгебраических уравнений

с трехдиагональной матрицей , т.е. с матрицей, все элементы которой,не лежащие на главной и двух побочных диагоналях, равны нулю при та

В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид

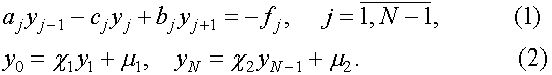
Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных.

Т.е. матрицу А можно записать

Идея метода прогонки состоит в следующем. Решение системы (1) ищется в виде

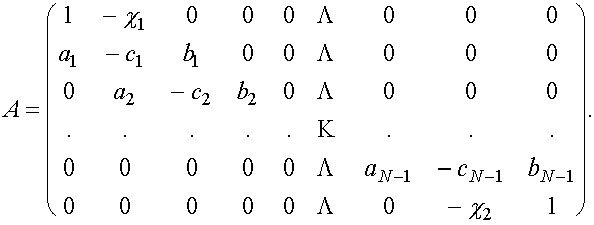
Рекомендуем скачать другие рефераты по теме: ответы школа, свобода реферат.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата