
Численные методы
| Категория реферата: Рефераты по математике
| Теги реферата: контрольные работы 9 класс, шпаргалки по экономике
| Добавил(а) на сайт: Карев.
Предыдущая страница реферата | 12 13 14 15 16 17 18 19 20 21 22 | Следующая страница реферата
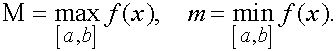 (11)
(11)
Тогд, так как ![]() то
то
![]()
и, следовательно,
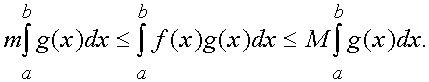
![]()
Если 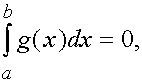 то
то 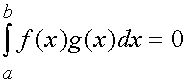 и в качестве
и в качестве ![]() можн взять любую точку из
можн взять любую точку из ![]()
Если 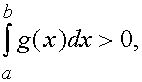 то вытекает существование такого числа с, удовлетворяющего неравенствам ( для этого делим все части
то вытекает существование такого числа с, удовлетворяющего неравенствам ( для этого делим все части ![]() на
на 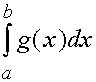 ):
):
![]() (12)
(12)
что
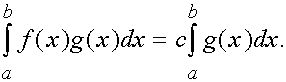 (13)
(13)
По теореме о промежуточных значениях непрерывной функции в силу (11) , (12) найдется точка ![]() , в которой
, в которой ![]() что вместе с равенством (13) доказывает теорему .
что вместе с равенством (13) доказывает теорему .
Теперь, так как ![]() то по доказанной теоремою
то по доказанной теоремою
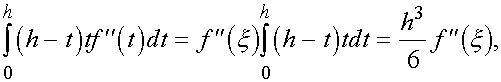
где ![]() - некоторая точка . Подставляя полученное в
- некоторая точка . Подставляя полученное в ![]() , приходим к формуле трапеций с остаточным членом :
, приходим к формуле трапеций с остаточным членом :
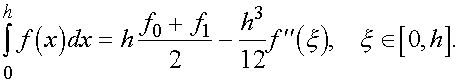 (14)
(14)
Формула Симпсона . Предположим, что ![]() Интеграл
Интеграл 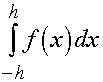 приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки
приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки ![]() де
де ![]()
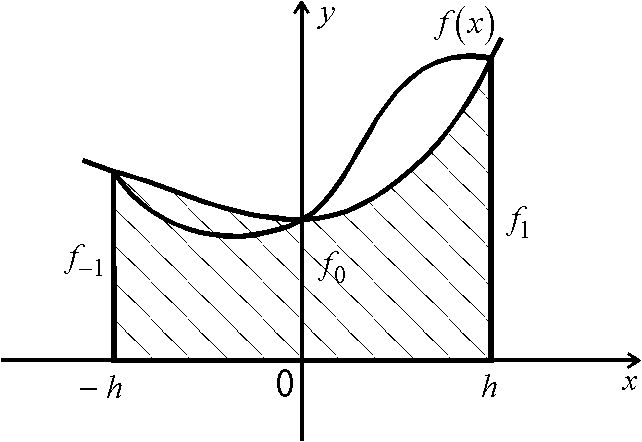
Указанная парабола задается уравнением
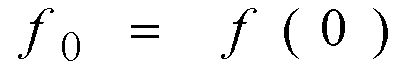
в чем нетрудно убедиться, положив поочередно ![]()
![]() (ее можно также получить, построив интерполяционный многочлен второй степени и приводя подобные ) Отсюда находи ( проверить самостоятельно)
(ее можно также получить, построив интерполяционный многочлен второй степени и приводя подобные ) Отсюда находи ( проверить самостоятельно)
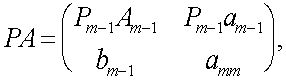
Таким образом , формула Симпсона , называемая также формулой парабол , имеет вид
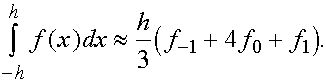 (15)
(15)
Положим ![]() где
где ![]() -функция (4). Поскольку
-функция (4). Поскольку
![]()
то согласно формул Тейлора с остаточным членом в интегральной форме имеем
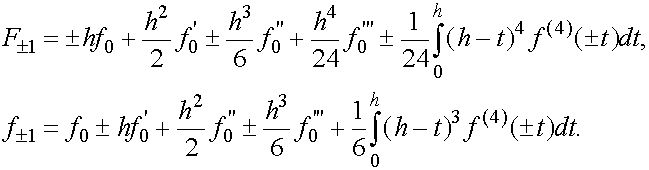 Отсюда получаем
Отсюда получаем
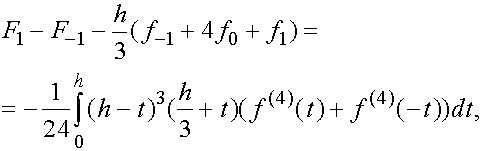 (16)
(16)
т.к. остальные члены взаимно уничтожаются.
Поскольку 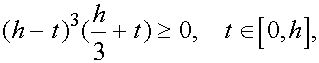 то применяя к интегралу (16) теорему 1 , а затем к полученному результату лемму, находим
то применяя к интегралу (16) теорему 1 , а затем к полученному результату лемму, находим

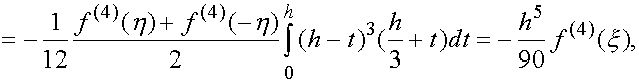 (17)
(17)
где ![]() нектрые точки.
нектрые точки.
Принимая во внимание, что 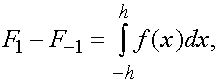 из (16), (17) приходим к формуле
из (16), (17) приходим к формуле
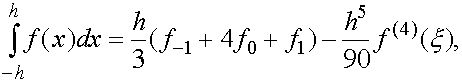 (18) т.е. к формуле Симпсона с остаточным членом.
(18) т.е. к формуле Симпсона с остаточным членом.
Рассмотрим квадратурные формулы прямоугольников (3), трапеций (7) и Симпсона (15) называются каноничными.
Усложненные квадратурные формулы.
На практике, если требуется вычислить приближенно интеграл (1) , обычно делят заданный отрезок ![]() на
на ![]() равных частей и на кождом частичном отрезке применяют какую-либо одну каноничную квадратурную формулу, а затем суммируют полученные результаты. Построенная таким путем квадратурная формула на отрезке
равных частей и на кождом частичном отрезке применяют какую-либо одну каноничную квадратурную формулу, а затем суммируют полученные результаты. Построенная таким путем квадратурная формула на отрезке ![]() называется усложненной. При применении формул прямугольников и трапеций длину частичных отрезков удобно применять за
называется усложненной. При применении формул прямугольников и трапеций длину частичных отрезков удобно применять за ![]() , а при использовании формулы Симпсона - за
, а при использовании формулы Симпсона - за ![]() .
.
Остановимся сначала на применении формулы прямоугольников. Пусть ![]() Обозначим частичные отрезки через
Обозначим частичные отрезки через ![]()
где 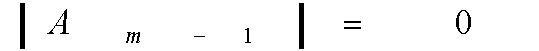
В соответствии с (3) полагаем
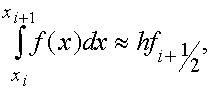 (19)
(19)
где 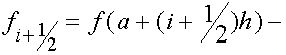 значение
значение ![]() в середине частичного отрезка
в середине частичного отрезка ![]() . При этом справедливо аналогичное (6) равенство
. При этом справедливо аналогичное (6) равенство
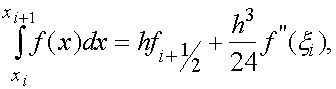 (20) где
(20) где ![]() некоторая точка.
некоторая точка.
Суммирование по всем частичным отрезкам приближенного равенства (19) приводит к усложненной квадратурной формуле прямоугольников:
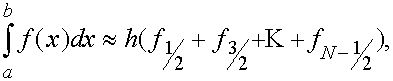 (21)
(21)
а суммирование равенств (20) с учетом того,что по лемме
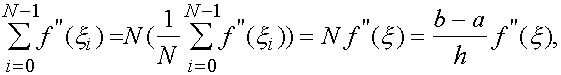
где ![]() -некоторая точка отрезка
-некоторая точка отрезка ![]() , дает усложненную формулу прямоугольников с остаточным членом:
, дает усложненную формулу прямоугольников с остаточным членом:
Рекомендуем скачать другие рефераты по теме: ответы школа, свобода реферат.
Категории:
Предыдущая страница реферата | 12 13 14 15 16 17 18 19 20 21 22 | Следующая страница реферата
 Главная
Главная