Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Данное определение вероятности через благоприятствующие равновозможные непересекающиеся события называют часто классическим определением вероятности. Оно подтверждается на практике в виде закона больших чисел. Он проявляется следующим образом. Если сделать большое число n* испытаний, в каждом из которых может появиться событие A, то в результате оказывается, что число m* появлений события A оказывается как правило очень близким к величине Р(A), то есть выполняется с вероятностью очень близкой к единице – практически обязательно, с большой степенью точности приближенное равенство

m*/n* ≈ m/n=Р(A)(2.2)

Условной вероятностью события А по событию В называют величину Р(А|В), которая дает равенство Р(А∩В)=Р(A|B)·P(B). Смысл этого определения таков. Условная вероятность оценивает шансы осуществления события А, когда известно, что произошло событие В.

События А и В называются независимыми, если Р(A|B)=P(A). Тогда Р(А∩В)=Р(A)·P(B). Иначе говоря, события А и В независимы, когда вероятность осуществления события А не зависит от того, осуществилось или нет событие В. И наоборот, вероятность осуществления события В не зависит от осуществления события А.

Например, пусть бросают две не связанные друг с другом игральные кости. Пусть событие А–на первой кости выпало 4 очка. Событие В–на второй кости выпало 2 очка. Тогда Р(А)=1/6,Р(В)=1/6. События А и В естественно полагать независимыми. Стало быть, полагаем Р(А|B)=P(A), P(B|A)=P(B) и P(А∩В)=P(A)·P(B)=1/6·1/6=1/36. То есть вероятность события С=А∩В – на первой кости выпало 2 очка и при этом на второй кости выпало 4 очка равна 1/36.

Несколько событий A1,A2,…,Ak называются независимыми в совокупности, если Р(∩Ai)=Р(A1)·Р(A2)·…·Р(Ak). Важно заметить, что из попарной независимости всех событий Аi и Aj, i=1,…,k, j=1,…,k, i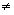j, вообще говоря, не следует независимость событий A1,A2,…,Ak в совокупности. В этом можно убедиться на конкретном примере.

Подчеркнем еще раз, что физической основой для теории вероятностей является следующее статистическое свойство устойчивости частот. Буквой А обозначим случайное событие, связанное с некоторым повторяющимся опытом. Пусть опыт повторяется n* раз при одинаковых условиях. Пусть 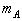*–число появлений событий А. Относительная частота 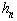появления событий А определяется формулой

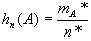(2.3)

Если неограниченно увеличивать число повторений опыта 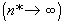, то относительная частота 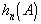будет устойчиво приближаться к некоторой фиксированной величине Р(А) и отклоняться от нее тем меньше и реже, чем больше n*. Эта величина и является вероятностью P события А. Если в теории вероятность Р(А) определена правильно, то оказывается, что теоретическое число Р(А) совпадает с описанным выше практическим пределом. Это обстоятельство и позволяет численно оценивать вероятность случайного события в теории.

3.Формула Бейеса.

Пусть мы знаем вероятности событий А и В: Р(А) и Р(В). И пусть мы знаем условную вероятность события А по В: Р(A|B). Как найти условную вероятность P(B|A). На этот вопрос отвечает формула Бейеса.

Р(B|A)=P(A|B)·P(B)/P(A)(3.1)

Разумеется этой формулой можно пользоваться только при условии, что Р(А)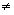0.

Формула Бейеса выводится из следующих равенств

Р(В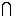А)=Р(В|A)·P(A)(3.2)

Р(A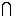B)=Р(A|B)·P(B)(3.3)

причем

Р(В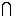А)=Р(A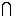B)(3.4)

так как пересечение событий В и А очевидно не зависит от порядка, в котором записаны А и В, т.е. В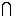А=A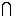B. В случае Р(А)=0 принимаю обычно, что Р(В|A) есть величина неопределенная.

4.Формула полной вероятности.

Пусть имеем полную группу из n попарно непересекающихся событий 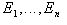. То есть

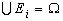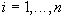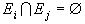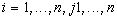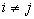, (4.1) , , (4.2)

Пусть мы знаем условные вероятности некоторого события А по Еi: Р(А|Ei) и вероятности Р(Ei), i=1,…,n. Справедлива следующая формула полной вероятности для события А

Р(А)=Р(A|E1)·P(E1)+…+P(A|En)·P(En)(4.3)

Доказательство этой формулы вытекает из следующих равенств

P(A)=P(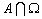)=P(A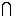(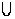Ei))=P(A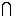E1)+…+P(A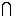En)=

=Р(A|E1)·P(E1)+…+P(A|En)·P(En)(4.4)

Из элементарной формулы Бейеса (3.1) и формулы полной вероятности (4.3) вытекает следующая более полная формула Бейеса

Р(Еi|A)=P(A|Ei)·P(Ei)/(Р(A|E1)·P(E1)+…+P(A|En)·P(En))(4.5)

Рекомендуем скачать другие рефераты по теме: российская федерация реферат, антикризисное управление предприятием.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата