
Теория Вероятностей
| Категория реферата: Рефераты по математике
| Теги реферата: дипломная работа методика, купить диплом о высшем образовании
| Добавил(а) на сайт: Shelagin.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
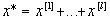 (10.4)
(10.4)
тогда математическое ожидание E(x*) равно сумме математических ожиданий Е(х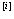 )
)
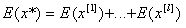 (10.5)
11.Дисперсия случайной величины.
(10.5)
11.Дисперсия случайной величины.
Дисперсией D(x) случайной величины х называют число, которое определяется по формуле
D(x)=E(x–E(x))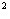 (11.1)
(11.1)
Поэтому дисперсия D(x) случайной величины х, которая может принимать значения 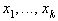 с вероятностями Р
с вероятностями Р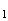 ,…Р
,…Р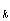 определяется, как число i=k i=k j=k
определяется, как число i=k i=k j=k
D(x)=∑(x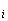 –E(x))
–E(x))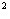 ∙P
∙P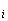 =∑(x
=∑(x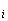 –
–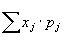 )
)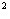 ∙P
∙P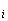 (11.2)
(11.2)
i=1 i=1 j=1
Например, в случае с игральной костью для дисперсии D(x) получаем следующее число
D(x)=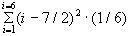 =(1/6)∙((1-7/2)
=(1/6)∙((1-7/2)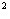 +(2-7/2)
+(2-7/2)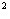 +(3-7/2)
+(3-7/2)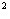 +(4-7/2)
+(4-7/2)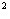 +(5-7/2)
+(5-7/2)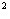 +(6-7/2)
+(6-7/2)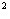 )=(1/6)∙(25/4+9/4+1/4+1/4+9/4+25/4)=(1/6)∙(35/2)=35/12(11.3)
)=(1/6)∙(25/4+9/4+1/4+1/4+9/4+25/4)=(1/6)∙(35/2)=35/12(11.3)
Пусть некоторая случайная величина х* является суммой (10.4) случайных величин 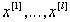 . Пусть эти случайные величины независимы. Это означает, что вероятность, с которой может осуществиться то или иное значение случайной величины
. Пусть эти случайные величины независимы. Это означает, что вероятность, с которой может осуществиться то или иное значение случайной величины 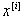 не зависит от того, какое значение принимают другие случайные величины
не зависит от того, какое значение принимают другие случайные величины 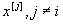 . Тогда доказывается, что дисперсия случайной величины х* является суммой дисперсии случайных величин
. Тогда доказывается, что дисперсия случайной величины х* является суммой дисперсии случайных величин 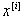
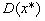
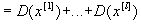 (11.4)
(11.4)
Важно заметить, что если случайные величины не являются независимыми, то дисперсия их суммы не обязательно равна сумме их дисперсий.
12.Закон больших чисел. В этом разделе приведу аккуратную формулировку закона больших чисел, которая восходит к замечательному математику нашей страны П.Л.Чебышеву. Пусть имеем некоторую случайную величину х. Выберем какое-нибудь положительное число М. Отберем те значения 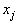 случайной величины х, для которых выполняется условие
случайной величины х, для которых выполняется условие
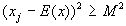 (12.1)
(12.1)
Из выражения для дисперсии (11.2) и из неравенства (12.1) вытекает следующее неравенство
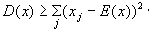 Р
Р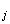
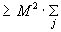 Р
Р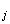
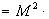 Р
Р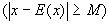 (12.2)
(12.2)
Здесь суммирование в (12.2) выполняется по тем индексам j, для которых выполнено неравенство.
Предположим теперь, что произведено n независимых испытаний. Пусть в i-том испытании осуществляется значение случайной величины 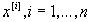 . Пусть математические ожидания и дисперсии всех этих независимых случайных величин одинаковы. Тогда согласно материалу из разделов 10,11 для суммы
. Пусть математические ожидания и дисперсии всех этих независимых случайных величин одинаковы. Тогда согласно материалу из разделов 10,11 для суммы
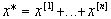 (12.3)
(12.3)
этих случайных величин и из (12.2) получаем следующее неравенство
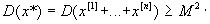 Р
Р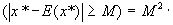
·Р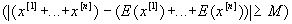 (12.4)
(12.4)
Так как случайные величины 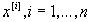 независимы, то дисперсия их суммы равна сумме их дисперсий. Кроме того, все дисперсии
независимы, то дисперсия их суммы равна сумме их дисперсий. Кроме того, все дисперсии 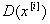 равны друг другу
равны друг другу 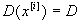 и все математические ожидания
и все математические ожидания 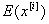 тоже равны друг другу
тоже равны друг другу 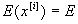 . Поэтому из (12.4) получаем неравенство
. Поэтому из (12.4) получаем неравенство
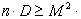 Р
Р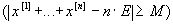 (12.5)
(12.5)
Введем число ε=M/n. Тогда из (12.5) получаем неравенство
Р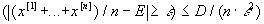 (12.6)
(12.6)
Отсюда для противоположного события
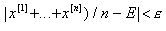 (12.7)
(12.7)
из (12.6) получаем следующее неравенство П.Л.Чебышева
Р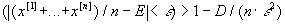 (12.8)
(12.8)
Таким образом, из (12.8) получается закон больших чисел П.Л.Чебышева:
Для любого сколь угодно малого положительного числа ε и числа β<1 найдется такое число N, что при числе испытаний n>N, будет справедливо неравенство
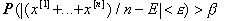 (12.9)
(12.9)
Рекомендуем скачать другие рефераты по теме: российская федерация реферат, антикризисное управление предприятием.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
 Главная
Главная