Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

2.4. Классификация положений равновесия системы второго порядка.

Исследуем на устойчивость положения равновесия линейной однородной системы двух уравнений с постоянными коэффициентами. Пусть , где . Как было показано в пункте 1.4, тип особой точки такой системы определяется корнями характеристического уравнения  или . Его корни можно найти по формуле

.

Рассмотрим следующие случаи согласно пункту 1.4.

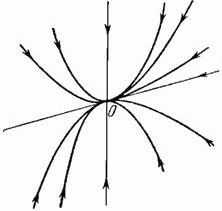
1)  вещественны, различны и  (). Параметрические уравнения траекторий: . Положение равновесия называется узел. Если корни  положительны (), то решения будут неограниченно возрастать, и особая точка — неустойчивый узел.

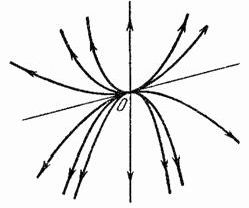
Если  отрицательны (), то решения с ростом времени будут неограниченно уменьшаться, то есть положение равновесия будет асимптотически устойчивым. Особая точка — устойчивый узел.

                    

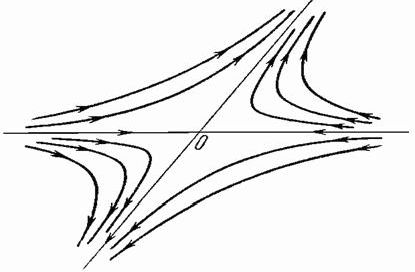
2)  вещественны и  (). В этом случае одна из траекторий всегда будет неограниченно возрастать, а другая неограниченно уменьшаться. Таким образом, седло всегда неустойчиво.

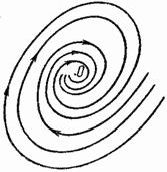
3)  комплексно-сопряженные, но не чисто мнимые (). Решение в полярных координатах запишется в виде , где . Если  (), то спирали будут раскручиваться от особой точки, и фокус будет неустойчивым.

Если  (), то особая точка — устойчивый фокус, причем устойчивость асимптотическая.

                  

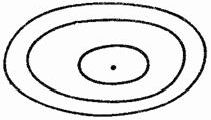
4)  (). Особая точка — центр, траектории — окружности, то есть положение равновесия является устойчивым, но не асимптотически.

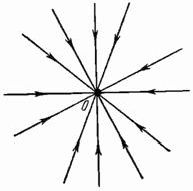
5) . Если , то получаем неустойчивый узел, либо вырожденный, либо дикритический. Если , положение равновесия будет асимптотически устойчивым.

                   

6) Один из корней равен нулю (например ). Траекториями являются прямые, параллельные друг другу. Если , то получаем прямую неустойчивых особых точек. Если , то прямая будет содержать устойчивые особые точки.

7) Оба корня равны нулю. Тогда . Особая точка неустойчива.

Пример. Рассмотрим систему . Положение равновесия находится из уравнения , или , откуда . Следовательно, положение равновесия — неустойчивый узел. Жорданова форма матрицы А имеет вид:

.

Найдем координаты преобразования , приводящего матрицу А к жордановой форме, то есть переводящего систему к виду . Дифференцируя эти уравнения и подставляя в исходную систему, получаем:

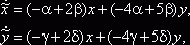
откуда с учетом  ,  — произвольное, ,  — произвольное. Получаем преобразование . Определим новое положение осей:

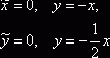
Решение системы  запишется в виде , а исходной системы отсюда 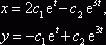. Схематическое изображение траекторий:

Рекомендуем скачать другие рефераты по теме: решебник по физике, работа реферат.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата