Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

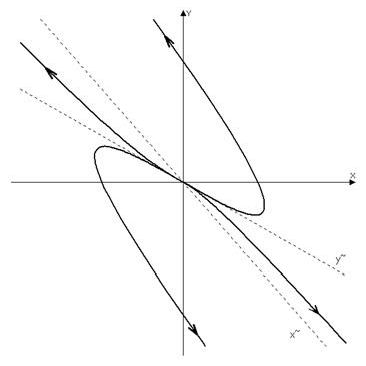
Рассмотрим теперь некоторые положения равновесия в трехмерном пространстве. Характеристическое уравнение — кубическое с вещественными коэффициентами, оно может иметь три вещественных или один вещественный и два комплексно-сопряженных корня. В зависимости от расположения этих корней  на плоскости  возможно 10 "грубых" случаев (рис. 3, 1)-5) и 1')-5')) и ряд "вырожденных" (рис. 3, 6)-9)), когда вещественная часть одного из корней равна нулю или вещественной части не сопряженного с ним корня. Случаи кратных корней здесь не рассматриваются.

Поведение фазовых траекторий в приведенных случаях показано на рис. 4. Случаи 1')-5') получаются из случаев 1)-5) изменением направления оси t, так что на рис. 4 надо лишь заменить все стрелки на противоположные.

Устойчивость по Ляпунову в рассмотренных случаях следующая. Все случаи 1')-5'), а также 2), 5), 8) и 9) неустойчивы. Случаи 1), 3) и 4) устойчивы асимптотически. Случай 6) устойчив.

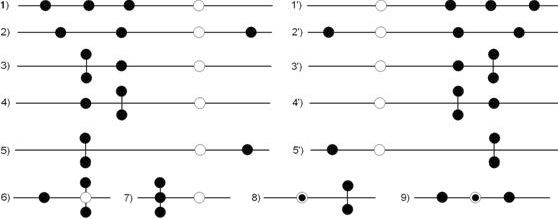
Рис. 3. Собственные числа матрицы А. Закрашенным кружком отмечены ,

светлым — начало координат.

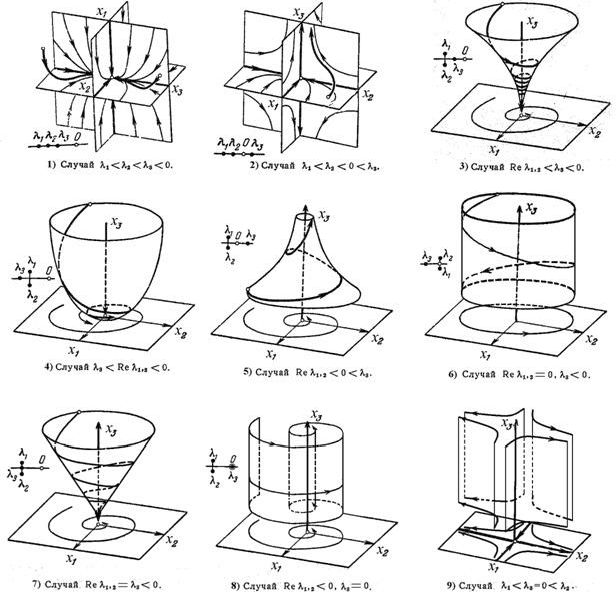
Рис. 4. Фазовые кривые в трехмерном пространстве.

2.5. Автономные системы на плоскости. Предельные циклы.

Рассмотрим автономную двумерную систему

  ,        (5)

где  — область.

Предположим, что система (5) имеет замкнутую траекторию  с наименьшим периодом . Возьмем произвольную точку  и проведем через нее нормаль  к  единичной длины. Для определенности считаем, что  направлен во внешнюю область. Не нарушая общности, считаем также, что  — начало координат (этого можно добиться заменой ). Точки на нормали  определяются единственной координатой . В качестве  берем расстояние от точки нормали до начала координат, если точка лежит снаружи , и это расстояние, взятое с обратным знаком, если она лежит внутри .

Рассмотрим траектории , проходящие через точки нормали. Запишем уравнение

               (6)

с неизвестными t, s ( — параметр).

Лемма 3. Существует  такое, что в области  уравнение (6) имеет единственное решение , удовлетворяющее условиям , причем функции  непрерывно дифференцируемы при .

Доказательство. Так как  — решение с периодом , то по теореме о дифференцируемости решения функция  определена и непрерывно дифференцируема по t и  в некоторой окрестности точки . Тогда функция  определена и непрерывно дифференцируема в некоторой окрестности точки . Так как  -периодична, то . Рассмотрим якобиан  в точке . Имеем . Следовательно, в точке  , поскольку  и  — ортогональные векторы. Тогда утверждение леммы вытекает из теоремы о неявной функции.

Следствие. Справедлива формула

  .

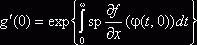Выясним геометрический смысл функций . Лемма 3 утверждает, что каждая траектория, пересекающая нормаль  в точке  из -окрестности начала координат, вновь пересечет ее через промежуток времени  в точке . При этом так как функция  также делает полный оборот вдоль  при , то траектория  также делает полный оборот при , оставаясь в малой окрестности , если  достаточно мало.

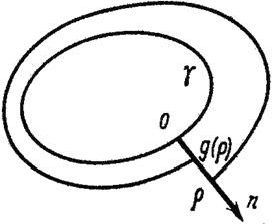
Функция  называется функцией последования.

Определение. Замкнутая траектория  автономного уравнения (5) называется устойчивым предельным циклом, если существует такое , что  является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой .

Рекомендуем скачать другие рефераты по теме: решебник по физике, работа реферат.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата