Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Определение. Замкнутая траектория  автономного уравнения (5) называется неустойчивым предельным циклом, если существует такое , что  является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой .

Так как в реальной действительности время течет в положительном направлении, то на практике реализуются те периодические движения, которым соответствуют устойчивые предельные циклы. Такие движения называются автоколебаниями.

Теорема 4. Пусть 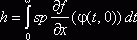.      (7)

Если , то  является устойчивым предельным циклом; если , то  — неустойчивый предельный цикл.

Характер приближения соседних траекторий к  при  следующий: они приближаются к , образуя бесконечное число витков спирали, как изнутри, так и снаружи.

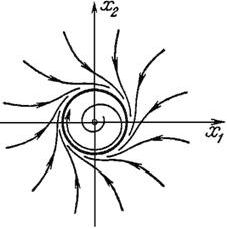
2.6. Устойчивость по первому приближению.

Вернемся к рассмотрению уравнения (1), где . После замены  получим уравнение (2), которое, используя разложение в ряд Тейлора, запишем в виде

  ,   (8)

где  при . (9)

Теорема 5. Пусть  — постоянная матрица, предельный переход в (9) выполняется равномерно по  и вещественные части собственных чисел матрицы  отрицательны. Тогда решение  уравнения (8) асимптотически устойчиво.

Теорема 6. Пусть  — постоянная матрица, предельный переход в (9) выполняется равномерно по . Для устойчивости по Ляпунову нулевого решения уравнения (8) необходимо, чтобы вещественные части собственных чисел матрицы  были неположительны.

Рассмотрим теперь автономное уравнение (1): ,            (10)

где функция  непрерывно дифференцируема при , причем . Тогда  является положением равновесия уравнения (10). После замены  уравнение (10) принимает вид , где , функция  непрерывно дифференцируема при  и

   при .     (11)

Из (11) и теорем 5 и 6 вытекает следующее утверждение.

Теорема 7. Если все собственные числа матрицы  имеют отрицательные вещественные части, то положение равновесия  асимптотически устойчиво; если же хоть одно из собственных чисел имеет положительную вещественную часть, то оно неустойчиво.

Пример. Рассмотрим систему двух уравнений  Координаты положений равновесия определяются из уравнений . Положения равновесия:

Соответствующие матрицы  имеют вид

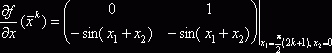, или .

Собственные числа определяются уравнением . При k четном , при k нечетном . По теореме 7 при k четном решения  асимптотически устойчивы, а при k нечетном неустойчивы.

Предположим теперь, что правая часть уравнения (1) и решение  периодичны по t с одним и тем же периодом . Тогда в уравнении (8) , . Далее, так как  равномерно непрерывна на компакте , то в силу периодичности   выполняется равномерно по . Поскольку  — периодическая матрица, то существует замена переменных ,          (12)

где  — периодическая с периодом  функция класса , причем , переводящая уравнение  в  с постоянной матрицей коэффициентов , определяемой теоремой Флоке. Следовательно, замена (12) переводит (8) в уравнение

  ,         (13)

Рекомендуем скачать другие рефераты по теме: решебник по физике, работа реферат.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата