Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Выше говорилось о том, что если для двух случайных величин X и Y имеет место равенство P(X Ç Y) = P(X)· P(Y), то эти величины считаются независимыми. Ну, а если это не так!?

Ведь всегда важно знать: насколько зависит одна СВ от другой? Дело не только в присущем людям стремлении анализировать что-либо обязательно в числовом измерении. Уже понятно, что прикладная статистика требует непрерывных вычислений, что использование компьютера вынуждает нас работать с числами, а не с понятиями.

Для числовой оценки взаимосвязи между двумя СВ: Y – с известными M(Y) и s y

и X – с M(X) и s x принято использовать так называемый коэффициент корреляции

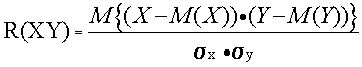. {3–1}

Обратим внимание на способ вычисления коэффициента корреляции. В числителе находится математическое ожидание произведения отклонений величин X и Y от собственных математических ожиданий.

Этот коэффициент может принимать значения от –1 до +1 — в зависимости от тесноты и характера связи между данными СВ.

Если коэффициент корреляции равен нулю, то X и Y называют некоррелированными. Считать их независимыми обычно нет оснований — оказывается, что существуют такие, как правило — нелинейные связи величин, при которых коэффициент корреляции равен нулю, хотя величины зависят друг от друга.

Обратное всегда верно — если величины независимы, то R(XY) = 0. Но, если модуль R(XY) равен 1, то есть все основания предполагать наличие линейной связи между Y и X. Именно поэтому часто говорят о линейной корреляции при использовании такого способа оценки связи между СВ.

Если у нас имеется ряд наблюдений за двумя случайными величинами, то можно оценить выборочное значение коэффициента корреляции –

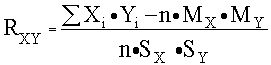{3–2}

Оценку корреляционной связи двух СВ можно производить и без учета их дисперсий.

Числитель коэффициента корреляции

. {3–3}

называют ковариацией случайных величин, которая также служит мерой связи, но без непосредственного учета дисперсий.

Различие между такими двумя показателями парной связи СВ достаточно существенное.

· Коэффициент корреляции определяет степень, тесноту линейной связи между величинами и является безразмерной величиной.

· Ковариация двух СВ определяет эту связь безотносительно к ее виду и является величиной размерной.

Множественная корреляция

В ряде случаев статистического анализа приходится решать вопрос о связях нескольких (более 2) СВ или вопрос о множественной корреляции.

Пусть X, Y и Z – случайные величины, имеющие математические ожидания M(X), M(Y), M(Z) и среднеквадратичные отклонения s x ,s y, s z соответственно. Тогда можно найти парные коэффициенты корреляции Rxy, Rxz, Ryz по приведенной выше формуле.

Но этого явно недостаточно – ведь мы на каждом из трех этапов попросту забывали о наличии третьей СВ! Поэтому в случаях множественного корреляционного анализа иногда требуется отыскивать т. н. частные коэффициенты корреляции — например, оценка виляния Z на связь между X и Y производится с помощью коэффициента

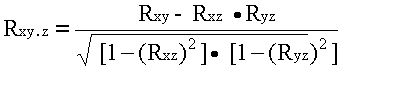
И, наконец, можно поставить вопрос — а какова связь между данной СВ и совокупностью остальных? Ответ на такие вопросы дают коэффициенты множественной корреляции RX.YZ, RY.XZ, RZ.XY, формулы для вычисления которых построены по тем же принципам — учету связи одной из величин со всеми остальными в совокупности.

Рекомендуем скачать другие рефераты по теме: скачать доклад бесплатно, вирусы реферат.





Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата