|
n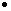 p p |
n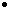 p p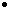 q q |
Sqrt(q/n·
p) |
|
Паскаля |
k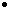 q/p q/p |
k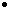 q/p2 q/p2 |
Sqrt(1/ kq) |
|
Геометрическое |
q/p |
q/p2 |
Sqrt(1/q) |
|
Пуассона |
l
|
l
|
Sqrt(1/l
) |
Можно ли предложить ещё один или несколько показателей – сжатых описаний распределения дискретной СВ? Разумеется, можно.
Первый показатель (математическое ожидание) и второй (дисперсия) чаще всего называют моментами распределения. Это связано со способами вычисления этих параметров по известному закону распределения – через усреднение значений самой СВ или усреднение квадратов ее значений.
Конечно, можно усреднять и кубы значений, и их четвертые степени и т.д., но что мы при этом получим? Поищем в теории ответ и на эти вопросы.
Начальными моментами k-го порядка случайной величины X обычно называют суммы:
n
k = S
(X i)k ·
P(X i); n
0 = 0; {2–7}
а центральными моментами – суммы:
m
k= S
(X i –n
1)k ·
P(X i), {2–8} при вычислении которых усредняются отклонения от центра распределения – математического ожидания.
Таким образом,
·
m
1 = 0;
·
n
1 = M(X) является параметром центра распределения;
·
m
2 = D(X) является параметром рассеяния; {2-9}
·
n
3 и m
3 – описывают асимметрию распределения;.
·
n
4 и m
4 – описывают т.н. эксцесс (выброс) распределения и т.д.
Иногда используют еще один показатель степени разброса СВ – коэффициент вариации V= s
/ M(X), имеющий смысл при ненулевом значении математического ожидания.
Распределения непрерывных случайных величин
До этого момента мы ограничивались только одной “разновидностью” СВ – дискретными, т.е. принимающими конечные, заранее оговоренные значения на любой из шкал Nom, Ord, Int или Rel .
Рекомендуем скачать другие рефераты по теме: скачать доклад бесплатно, вирусы реферат.
Предыдущая страница реферата |
6
7
8
9
10
11
12
13
14
15
16 |
Следующая страница реферата
 Главная
Главная