Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата

Для этого достаточно установить, что ряд справа равномерно сходится. Прежде всего, оценим . Имеем

откуда

Оценим теперь . По неравенству С.Н.Бернштейна,

Пользуясь этой оценкой, получаем:

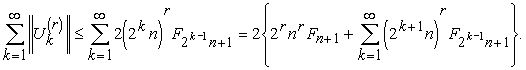
Но

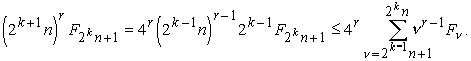
Поэтому

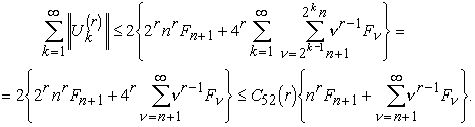(6.21)

Итак, доказана сходимость ряда , а вместе с этим установлена и формула (6.20). Из (6.20) и (6.21) вытекает, что

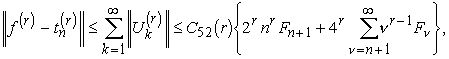
и теорема доказана.

В некоторых случаях оценка (6.18) может быть упрощена. Пусть, например,

(6.22)

Тогда

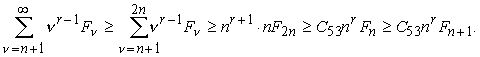
Поэтому при выполнении условия (6.22) вместо (6.18) можно написать

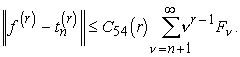
Следствие 10.1. Пусть r-натуральное число и сходится ряд

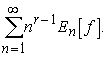
Тогда

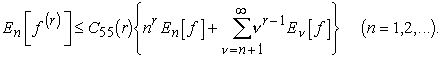(6.23)

Теорема 11. Пусть r-натуральное число и для функции f сходится ряд

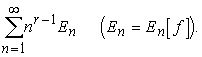
Тогда для любого натурального k и любого

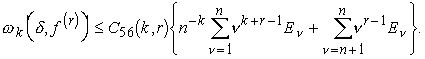(6.24)

Доказательство. Имеем

Отсюда, по лемме 10,

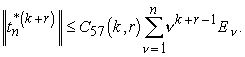
Далее, согласно теореме 10,

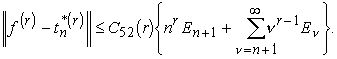
Воспользуемся теперь леммой 9. Получаем

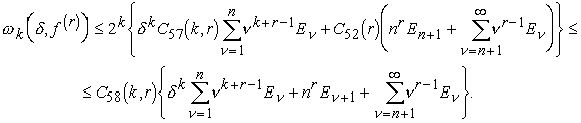
Заметим, что

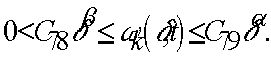
Таким образом, если , то

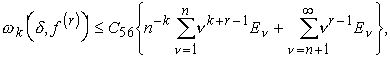
и теорема доказана.

§7. Основная теорема.

Обратимся теперь к рассмотрению следующего вопроса: каковы необходимые и достаточные условия того, чтобы

где -заданная невозрастающая функция?

Насколько нам известно, эта задача не была до сих пор решена даже для случая . Мы решим её для функций сравнения .

Лемма 11. Пусть и для некоторого натурального

(7.1)

Рекомендуем скачать другие рефераты по теме: аристотель реферат, международный реферат.





Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата