
Модель портального манипулятора
| Категория реферата: Рефераты по науке и технике
| Теги реферата: доклад на тему, педагогические рефераты
| Добавил(а) на сайт: Кияк.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
и для звеньев заданной конфигурации являются известными константами. При отсутствии осевых симметрий тензор инерции звена в точке
|
|
(1.9) |
центробежные моменты в которой определяются выражениями
|
|
(1.10) |
и также являются известными константами.
Определим вектор скорости центра инерции звена i через проекции на оси связанной с ним системы координат как
|
|
(1.11) |
или через проекции на оси неподвижной системы осей в виде
|
|
(1.12) |
По аналогии с ![]() введем вектор угловой скорости звена
введем вектор угловой скорости звена
|
|
(1.13) |
и запишем равенство (1.6) в развернутой форме для случая, когда звенья манипулятора обладают симметрией относительно главных осей инерции. Для этого подставим выражения ![]() ,
, ![]() ,
, ![]() из (1.7), (1.11), (1.13) в (1.6) и получим
из (1.7), (1.11), (1.13) в (1.6) и получим
|
|
(1.14) |
При использовании вектора скорости центра инерции в форме (1.14) выражение
|
|
(1.15) |
с учетом которого равенство (1.4) принимает вид
|
|
(1.16) |
Построение динамической модели переходных процессов манипулятора МРЛ-901П
Модель переходных процессов в манипуляторе МРЛ-901П
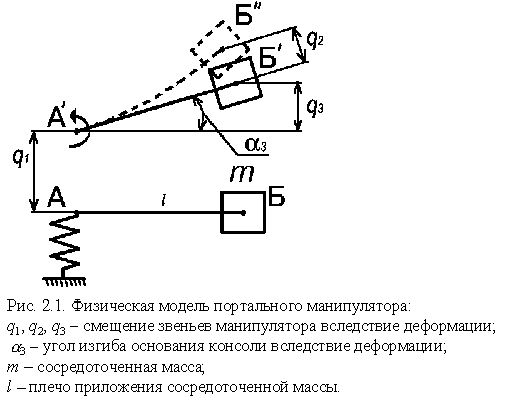
Модель портального манипулятора МРЛ-901П представлена на рис. 2.1. Деформирующимися элементами в манипуляторе являются: зубчатый ремень, обозначенный пружиной; консольная часть, на которой имеется сосредоточенная масса m. Деформация поперечной консоли обозначена на схеме углом ![]() . Исходными данными для расчета такой модели будут: значение подвижной массы m, плечо приложения этой массы l, а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.
. Исходными данными для расчета такой модели будут: значение подвижной массы m, плечо приложения этой массы l, а также коэффициент натяжения зубчатого ремня, определяемый как отношение прогиба ремня к его длине и влияющий на жесткость, и демпфирование модуля линейного перемещения.
При остановке электроприводов подвижные массы будут продолжать движение под действием инерционных сил, в результате чего точки А и Б займут положение ![]() и
и ![]() соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.
соответственно, затем остановятся и под действием сил упругой деформации пружины и балки начнут совершать колебательное движения.
Рассматриваемая модель имеет три степени свободы, обозначим независимые обобщенные координаты как ![]() ,
, ![]() и
и ![]() . Для описания данной модели воспользуемся уравнением Лагранжа второго рода:
. Для описания данной модели воспользуемся уравнением Лагранжа второго рода:
|
|
(2.1) |
где T - кинетическая энергия системы; Q - обобщенная сила; k - количество степеней свободы.
Кинетическая энергия системы с тремя степенями свободы является однородной квадратичной формой обобщенных скоростей [5]:
|
|
(2.2) |
Коэффициенты ![]() являются функциями координат
являются функциями координат ![]() ,
, ![]() и
и ![]() .
.
Предположим, что обобщенные координаты отсчитываются от положения равновесия, где ![]() .
.
Располагая коэффициенты ![]() по степеням и пологая для упрощения записи
по степеням и пологая для упрощения записи ![]() , получим:
, получим:
|
|
(2.3) |
Потенциальная энергия ![]() системы:
системы:
|
|
(2.4) |
При этом учитываем, что в положении равновесия ![]() обобщенные силы также обращаются в нуль.
обобщенные силы также обращаются в нуль.
Рекомендуем скачать другие рефераты по теме: социальная работа реферат, реферат здания.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
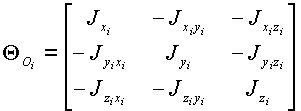 ,
,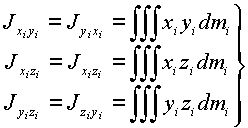
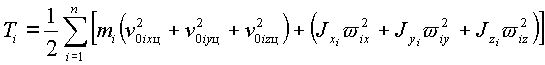 .
.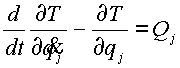 (j = 1,2,…,k),
(j = 1,2,…,k),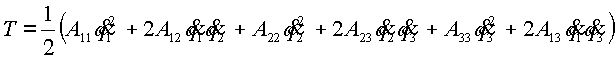 ,
,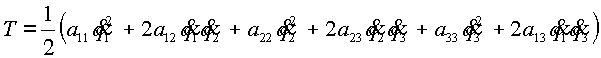
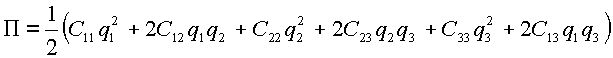
 Главная
Главная